题目内容
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
【答案】
(1)
解:作BD⊥AC于点D,如图所示:
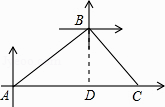
由题意可知:AB=30×1=30海里,∠BAC=30°,∠BCA=45°,
在Rt△ABD中,
∵AB=30海里,∠BAC=30°,
∴BD=15海里,AD=ABcos30°=15 ![]() 海里,
海里,
在Rt△BCD中,
∵BD=15海里,∠BCD=45°,
∴CD=15海里,BC=15 ![]() 海里,
海里,
∴AC=AD+CD=15 ![]() +15海里,
+15海里,
即A、C间的距离为(15 ![]() +15)海里.
+15)海里.
(2)
解:∵AC=15 ![]() +15(海里),
+15(海里),
轮船乙从A到C的时间为 ![]() =
= ![]() +1,
+1,
由B到C的时间为 ![]() +1﹣1=
+1﹣1= ![]() ,
,
∵BC=15 ![]() 海里,
海里,
∴轮船甲从B到C的速度为 ![]() =5
=5 ![]() (海里/小时).
(海里/小时).
【解析】(1)根据题意画出图形,再根据平行线的性质及直角三角形的性质解答即可.(2)根据甲乙两轮船从港口A至港口C所用的时间相同,可以求出甲轮船从B到C所用的时间,又知BC间的距离,继而求出甲轮船后来的速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目