题目内容
【题目】如图1,平面直角坐标系中,抛物线y= ![]() 与x 轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
与x 轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.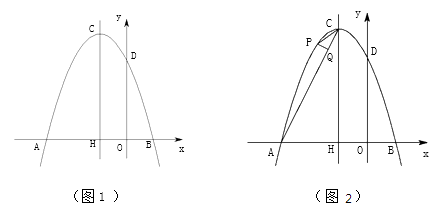
(1)求抛物线的表达式;
(2)点E,F 分别是抛物线对称轴CH 上的两个动点(点E 在点F 上方),且EF=1,求使四边形BDEF 的周长最小时的点E,F 坐标及最小值;
(3)如图2,点P 为对称轴左侧,x 轴上方的抛物线上的点,PQ⊥AC 交AC 于点Q,是否存在这样的点P 使△PCQ与△ACH 相似,若存在请求出点P 的坐标,若不存在请说明理由.
【答案】
(1)
将A(﹣3,0)、B(1,0),代入y=ax2+bx+3,
得: ![]()
解得:![]()
抛物线的解析式为:y=﹣x2﹣2x+3,
顶点C的坐标为(﹣1,4).
(2)
将D点向下平移1个单位,得点M,连接AM交对称轴于F,作DE∥FM交对称轴于E点,
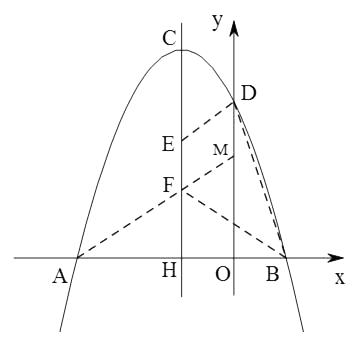
如图,EF∥DM,DE∥FM,四边形EFMD是平行四边形,
DE=FM,EF=DM=1.
DE+FB=FM+AF=AM.
由勾股定理,得AM=![]() =
=![]() ,
,
BD= ![]()
四边形BDEF周长的最小值=BD+DE+EF+FB
=BD+EF+(DE+BF)
= BD+EF +AM
=![]() +1+
+1+![]() ;
;
设AM的解析式为y=kx+b,将A、M点坐标代入解得k=![]() ,b=2.
,b=2.
AD的解析式为y= ![]() x+2,
x+2,
当x=﹣1时,y=![]() ,即F(﹣1,
,即F(﹣1, ![]() ),
),
由EF=1,得E(﹣1,![]() ),
),
当四边形BDEF周长最小时,此时点F(﹣1, ![]() ),E的坐标(﹣1,
),E的坐标(﹣1, ![]() ),
),
四边形BDEF周长的最小值是![]() +1+
+1+![]() .
.
(3)
点P在对称轴左侧.
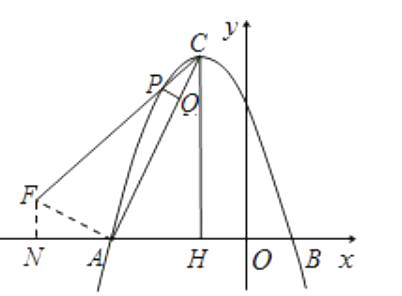
只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
由△CFA∽△CAH得 ![]() =2,
=2,
由△FNA∽△AHC得 ![]() .
.
∴AN=2,FN=1,点F坐标为(﹣5,1).
设直线CF的解析式为y=k2x+b2,则![]() ,
,
解得: 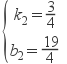 .
.
∴直线CF的解析式 ![]() ,
,
联立  ,
,
解得: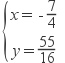 或 (舍去)
或 (舍去)![]() .
.
∴满足条件的点P坐标为 ![]() .
.
【解析】(1)二次函数解析系中有2个未知数,所以就需要2个点,将两点的坐标代进去即可求得;
(2)根据轴对称-求最短路径的方法去做;
(3)因为∠PCQ<∠CAH,所以只能是△PCQ∽△ACH,得∠PCQ=∠ACH.过A作CA的垂线交PC于点F,作FN⊥x轴于点N.

【题目】某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1= ![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?






