题目内容
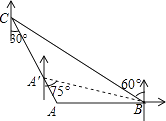
【题目】如图,AE平分∠CAD,AE∥BC,O为△ABC内一点,∠OBC=∠OCB.求证:∠ABO=∠ACO.

【答案】见解析
【解析】
根据平行线的性质,可得到:∠CAE=∠ACB,∠DAE=∠ABC,因为AE平分∠CAD,所以有:∠CAE=∠DAE,从而得到:∠ACB=∠ABC,又因为∠OBC=∠OCB,∠ABC=∠ABO+∠OBC,∠ACB=∠ACO+∠OCB,从而可得证,由此来解答本题即可.
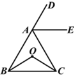
解:∵AE∥BC,
∴∠CAE=∠ACB,∠DAE=∠ABC,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∴∠ACB=∠ABC,
∵∠OBC=∠OCB,∠ABC=∠ABO+∠OBC,∠ACB=∠ACO+∠OCB,
∴∠ABO=∠ACO.

练习册系列答案
相关题目