题目内容
【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 . (只填写序号)
【答案】③⑤
【解析】解:如图, 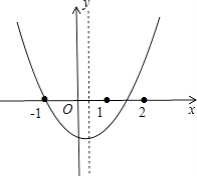
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①的结论正确;
∵抛物线过点(﹣1,0)和(m,0),且1<m<2,
∴0<﹣ ![]() <
< ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() >0,∴a+b>0,所以②的结论正确;
>0,∴a+b>0,所以②的结论正确;
∵点A(﹣3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,
∴y1>y2,所以③的结论错误;
∵抛物线过点(﹣1,0),(m,0),
∴a﹣b+c=0,am2+bm+c=0,
∴am2﹣a+bm+b=0,
a(m+1)(m﹣1)+b(m+1)=0,
∴a(m﹣1)+b=0,所以④的结论正确;
∵ ![]() <c,
<c,
而c≤﹣1,
∴ ![]() <﹣1,
<﹣1,
∴b2﹣4ac>4a,所以⑤的结论错误.
故答案为③⑤.
先根据题意画出抛物线的大致图像,观察函数图像的开口方向、对称轴的位置、抛物线与两坐标轴的位置可知:a>0,b<0,c<0,可对①作出判断;根据抛物线过点(﹣1,0)和(m,0),且1<m<2,结合对称轴方程可得出a+b>0,可对②作出判断;由点A(﹣3,y1),点B(3,y2)都在抛物线上,可根据两点到对称轴的距离远近对③作出判断;将(﹣1,0),(m,0),分别代入函数解析式,建立方程组,将两方程相减,再将方程变形即可对④作出判断;观察图像可知抛物线的顶点纵坐标<c,且c≤﹣1,建立不等式通过变形可对⑤作出判断。

 阅读快车系列答案
阅读快车系列答案