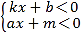题目内容
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
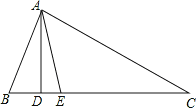
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
【答案】(1) 40°;(2) 20°;(3)能,20°.
【解析】
试题分析:(1)根据三角形内角和定理得∠BAC=180°-∠B-∠C=80°,然后根据角平分线定义得∠BAE=![]() ∠BAC=40°;
∠BAC=40°;
(2)由于AD⊥BC,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B+∠BAD,所以∠BAD=90°-∠B=20°,然后利用∠DAE=∠BAE-∠BAD进行计算;
(3)根据三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠BAE=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-![]() (∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°-∠B,然后利用角的和差得∠DAE=∠BAE-∠BAD=90°-
(∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°-∠B,然后利用角的和差得∠DAE=∠BAE-∠BAD=90°-![]() (∠B+∠C)-(90°-∠B)=
(∠B+∠C)-(90°-∠B)=![]() (∠B-∠C),即∠DAE的度数等于∠B与∠C差的一半.
(∠B-∠C),即∠DAE的度数等于∠B与∠C差的一半.
试题解析:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=40°;
∠BAC=40°;
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)=90°-
(180°-∠B-∠C)=90°-![]() (∠B+∠C),
(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-![]() (∠B+∠C)-(90°-∠B)=
(∠B+∠C)-(90°-∠B)=![]() (∠B-∠C),
(∠B-∠C),
∵∠B-∠C=40°,
∴∠DAE=![]() ×40°=20°.
×40°=20°.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案