题目内容
【题目】如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上.
(1)求证AE2+AD2=2AC2 ;
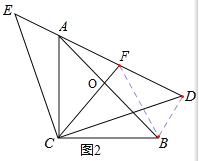
(2)如图2,过点C作CO垂直AB于0点并延长交DE于点F,请确定线段AE、AF、DF间的数量关系,并证明你的结论.

【答案】(1)见解析;(2)AF2=AE2+DF2,证明见解析.
【解析】
(1)根据等腰直角三角形的性质就可以得出△ACE≌△BCD,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
(2)连接BD、BF,由(1)可知∠FDB=90°,可得BF2=DF2+BD2=DF2+AE2, 又因为AC=BC,CO⊥AB,所以CF垂直平分AB,所以AF=BF,即可得出线段AE、AF、DF间的数量关系.
(1)如图,连接BD,
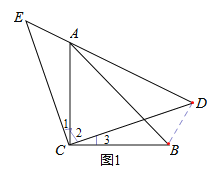
因为∠1+∠2=∠2+∠3=90°,所以∠1=∠3.
又因为CA=CB,CE=CD,所以△ACE≌△BCD(SAS),
所以BD=AE,∠BDC=∠E=45°,
所以∠CDE=45°,
所以∠ADB=45°+45°=90°,
所以AD2+BD2=AB2,即AD2+AE2=AB2.
又因为在Rt△ABC中,∠ACB=90°,可得AB2=AC2+BC2=2AC2,所以AE2+AD2=2AC2
(2)连接BD、BF,AF2=AE2+DF2,
在Rt△FDB中,∠FDB=90°,可得BF2=DF2+BD2=DF2+AE2,又因为AC=BC,CO⊥AB,所以CF垂直平分AB,所以AF=BF,所以AF2=AE2+DF2.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目