题目内容
【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.
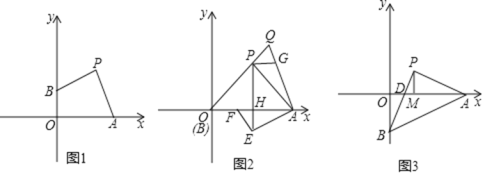
(一)发现:在如图1中,小红和小明都发现:∠AEC=∠A+∠C;
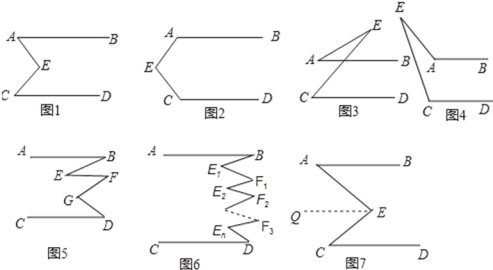
小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A( )
∵EQ∥AB,AB∥CD.
∴EQ∥CD( )
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:两人的证明过程中,完全正确的是 .
(二)尝试:
(1)在如图2中,若∠A=110°,∠C=130°,则∠E的度数为 ;
(2)在如图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(三)探索:
装置如图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(四)猜想:
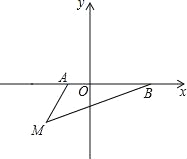
(1)如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(2)如图6,你可以得到什么结论?(直接写出结论)
【答案】(一) ( 两直线平行,内错角相等)(平行于同一条直线的两直线平行),小明的证法;(二)120°,30°;(三)见解析;(四) (1)∠E+∠G=∠B+∠F+∠D;(2)见解析.
【解析】
(一)小红、小明的做法,都是做了平行线,利用平行线的性质;(二)的(1)、(四)都可仿照(一),通过添加平行线把分散的角集中起来.
(一)( 两直线平行,内错角相等),(平行于同一条直线的两直线平行);
完全正确的是:小明的证法;
(二)尝试:
(1)(1)过点E作EF∥AB,
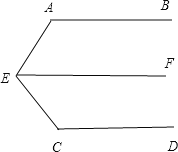
∵AB∥CD,
∴EF∥CD.∵EF∥AB,
∴∠A+∠AEF=180°,
∵∠A=110°,∴∠AEF=70°.
∵EF∥CD,
∴∠C+∠CEF=180°,
∵∠C=130°,∴∠CEF=50°.
∴∠AEC=∠AEF+∠CEF=70°+50°=120°.
(2)如图,

∵AB∥CD,
∴∠EOB=∠C=50°,
∵∠EOB=∠A+∠E,
∵∠E=∠EOB-∠A=50°-20°=30°.
答案:120°,30°.
(三)∠E=∠EAB∠C.
理由:延长EA,交CD于点F.
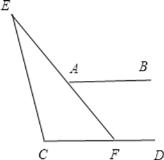
∵AB∥CD,
∴∠EFD=∠EAB.
∵∠EFD=∠C+∠E,
∴∠EAB=∠C+∠E,
∴∠E=∠EAB∠C.
(四)(1)可通过过点E、F、G分别做AB的平行线,得到结论:∠E+∠G=∠B+∠F+∠D.
(2)同上道理一样,可得到结论:∠E1+∠E2+…+∠En=∠F1+∠F2+…∠Fn+∠B+∠D.

【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?