题目内容
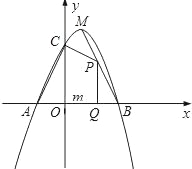
【题目】如图，已知二次函数y=﹣x2+bx+c（c＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB=OC=3，顶点为M．
（1）求二次函数的解析式；
（2）点P为线段BM上的一个动点，过点P作x轴的垂线PQ，垂足为Q，若OQ=m，四边形ACPQ的面积为S，求S关于m的函数解析式，并写出m的取值范围；
（3）探索：线段BM上是否存在点N，使△NMC为等腰三角形？如果存在，求出点N的坐标；如果不存在，请说明理由．
【答案】(1) 二次函数的解析式为y=﹣x2+2x+3；(2)S=﹣m2+
m+
（1≤m＜3）；(3) （
， 
）（1+
，4﹣
）（2，2）．
【解析】解：（1）∵OB=OC=3，
∴B（3，0），C（0，3）
∴
,
解得
,
∴二次函数的解析式为y=﹣x2+2x+3；
（2）y=﹣x2+2x+3=﹣（x﹣1）2+4，M（1， 4）
设直线MB的解析式为y=kx+n，
则有
,
解得
,
∴直线MB的解析式为y=﹣2x+6,
∵PQ⊥x轴，OQ=m，
∴点P的坐标为（m，﹣2m+6）
S四边形ACPQ=S△AOC+S梯形PQOC=
AOCO+
（PQ+CO）OQ（1≤m＜3）
=
×1×3+
（﹣2m+6+3）m=﹣m2+
m+
；
（3）线段BM上存在点N（
， 
），（2，2），（1+
，4﹣
）使△NMC为等腰三角形,
CM=
，CN=
，MN=
①当CM=NC时， 
，
解得x1=
，x2=1（舍去）
此时N（
， 
），
②当CM=MN时， 
，
解得x1=1+
，x2=1-
舍去），
此时N（1+
，4﹣
）.
③当CN=MN时， 
,
解得x=2，此时N（2，2）．
【题目】九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | …… |
月销量（件） | 200 | 180 | 160 | 140 | …… |
(1)已知该运动服的进价为每件60元，设售价为x元；
请用含有x的式子表示：
①销售该运动服每件的利润是 元；
②月销售量是 件；（直接写结果）
(2)设销售该运动服的月利润为y元，那么售价为多少元时，当月的利润最大？最大利润是多少？
