题目内容
【题目】如图,已知⊙![]() 半径为
半径为![]() ,从⊙
,从⊙![]() 外点
外点![]() 作⊙
作⊙![]() 的切线
的切线![]() 和
和![]() ,切点分别为点
,切点分别为点![]() 和点
和点![]() ,
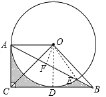
,![]() ,则图中阴影部分的面积是__________.
,则图中阴影部分的面积是__________.
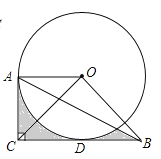
【答案】![]()
【解析】
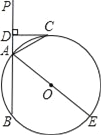
连接OD、OE,证明四边形ACDO是正方形 ,得出AC=OA=2,再求出∠ABC=30°,则∠OAB=∠ABC=30°,得出扇形OAE的圆心角为120°,作△AOE的高OF,求出OF与AE的长,利用面积公式即可求出阴影部分的面积.
连接OD、OE,
∵AC、BC是⊙![]() 的切线,
的切线,
∴OA⊥AC,OD⊥BC,AC=CD,
∴∠CAO=∠CDO=90°,
∴四边形ACDO是正方形
在Rt△ACB中,∵AC=OA=2,BC=![]() ,
,
∴AB=![]()
∴∠ABC=30°,
∵AO∥BC,
∴∠OAB=∠ABC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
过O作OF⊥AB于F,
∴OF=![]()
∴AF=![]() ,
,
∴AE=2![]() ,
,
S弓形ADE=S扇形OAE-S△AOE=![]()
∴S阴影=S△ACB- S弓形ADE=![]() -(
-(![]() )=
)=![]()

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目