ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ≈ΉΈοœΏy=ax+bx+4Θ®aΓΌ0Θ©ΙΐΒψA(1, ©¹1)Θ§B(5, ©¹1)Θ§”κy÷αΫΜ”ΎΒψC.
Θ®1Θ©«σ≈ΉΈοœΏ±μ¥ο ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§Ν§Ϋ”CBΘ§“‘CBΈΣ±ΏΉςCBPQΘ§»τΒψP‘Ύ÷±œΏBCœ¬ΖΫΒΡ≈ΉΈοœΏ…œΘ§QΈΣΉχ±ξΤΫΟφΡΎΒΡ“ΜΒψΘ§«“CBPQΒΡΟφΜΐΈΣ30Θ§
ΔΌ«σΒψPΉχ±ξ;
ΔΎΙΐ¥ΥΕΰΒψΒΡ÷±œΏΫΜy÷α”ΎF, ¥Υ÷±œΏ…œ“ΜΕ·ΒψG,Β±GB+![]() Ήν–Γ ±,«σΒψGΉχ±ξ.
Ήν–Γ ±,«σΒψGΉχ±ξ.
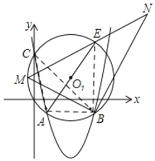
Θ®3Θ©»γΆΦ2Θ§Γ―O1ΙΐΒψAΓΔBΓΔC»ΐΒψΘ§AEΈΣ÷±ΨΕΘ§ΒψMΈΣ …œΒΡ“ΜΕ·ΒψΘ®≤Μ”κΒψAΘ§E÷ΊΚœΘ©Θ§ΓœMBNΈΣ÷±Ϋ«Θ§±ΏBN”κMEΒΡ―”≥ΛœΏΫΜ”ΎNΘ§«σœΏΕΈBN≥ΛΕ»ΒΡΉν¥σ÷Β
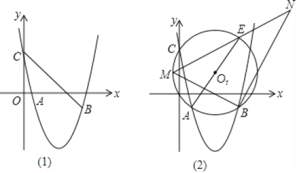
ΓΨ¥πΑΗΓΩΘ®1Θ©y=x©¹6x+4Θ®2Θ©ΔΌP(2, -4)ΜρP(3, -5) ΔΎG(0, -2)Θ®3Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―ΒψAΘ®1Θ§-1Θ©Θ§BΘ®5Θ§-1Θ©¥ζ»κ≈ΉΈοœΏy=ax2+bx+4ΫβΈω ΫΘ§Φ¥Ω…ΒΟ≥ω≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΔΌ»γΆΦΘ§Ν§Ϋ”PCΘ§ΙΐΒψPΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎRΘ§Ω…«σΒΟ÷±œΏBCΒΡΫβΈω ΫΈΣΘΚy=-x+4Θ§…ηΒψPΘ®tΘ§t2-6t+4Θ©Θ§RΘ®tΘ§-t+4Θ©Θ§“ρΈΣCBPQΒΡΟφΜΐΈΣ30Θ§Υυ“‘SΓςPBC=![]() ΓΝ(t+4t2+6t4)ΓΝ5ΘΫ15Θ§ΫβΒΟtΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ωΒψPΒΡΉχ±ξΘΜΔΎΒ±ΒψPΈΣΘ®2Θ§-4Θ© ±Θ§«σΒΟ÷±œΏQPΒΡΫβΈω ΫΈΣΘΚy=-x-2Θ§ΒΟFΘ®0Θ§-2Θ©Θ§ΓœGOR=45ΓψΘ§“ρΈΣGB+
ΓΝ(t+4t2+6t4)ΓΝ5ΘΫ15Θ§ΫβΒΟtΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ωΒψPΒΡΉχ±ξΘΜΔΎΒ±ΒψPΈΣΘ®2Θ§-4Θ© ±Θ§«σΒΟ÷±œΏQPΒΡΫβΈω ΫΈΣΘΚy=-x-2Θ§ΒΟFΘ®0Θ§-2Θ©Θ§ΓœGOR=45ΓψΘ§“ρΈΣGB+![]()
GF=GB+GRΘ§Υυ“‘Β±G”ΎF÷ΊΚœ ±Θ§GB+GRΉν–ΓΘ§Φ¥Ω…ΒΟ≥ωΒψGΒΡΉχ±ξΘΜΒ±ΒψPΈΣΘ®3Θ§-5Θ© ±Θ§Ά§άμΩ…«σΘΜ
Θ®3Θ©œ»”ΟΟφΜΐΖ®«σ≥ωsinΓœACB=![]() Θ§tanΓœACB=
Θ§tanΓœACB=![]() Θ§‘ΎRtΓςABE÷–Θ§«σΒΟ‘≤ΒΡ÷±ΨΕΘ§“ρΈΣMBΓΆNBΘ§Ω…ΒΟΓœN=ΓœAEB=ΓœACBΘ§“ρΈΣtanN=
Θ§‘ΎRtΓςABE÷–Θ§«σΒΟ‘≤ΒΡ÷±ΨΕΘ§“ρΈΣMBΓΆNBΘ§Ω…ΒΟΓœN=ΓœAEB=ΓœACBΘ§“ρΈΣtanN=![]() ΘΫ
ΘΫ![]() Θ§Υυ“‘BN=
Θ§Υυ“‘BN=![]() MBΘ§Β±MBΈΣ÷±ΨΕ ±Θ§BNΒΡ≥ΛΕ»Ήν¥σΘ°
MBΘ§Β±MBΈΣ÷±ΨΕ ±Θ§BNΒΡ≥ΛΕ»Ήν¥σΘ°
(1) ΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏy=ax2+bx+4Θ®aΓΌ0Θ©ΙΐΒψAΘ®1Θ§-1Θ©Θ§BΘ®5Θ§-1Θ©Θ§
Γύ![]() ΫβΒΟ
ΫβΒΟ![]()
Γύ≈ΉΈοœΏ±μ¥ο ΫΈΣy=x©¹6x+4Θ°
(2)ΔΌ»γΆΦΘ§Ν§Ϋ”PCΘ§ΙΐΒψPΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎRΘ§
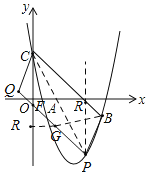
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+mΘ§
ΓΏBΘ®5Θ§-1Θ©Θ§CΘ®0Θ§4Θ©Θ§
Γύ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]()
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣΘΚy=-x+4Θ§
…ηΒψPΘ®tΘ§t2-6t+4Θ©Θ§RΘ®tΘ§-t+4Θ©Θ§
ΓΏCBPQΒΡΟφΜΐΈΣ30Θ§
ΓύSΓςPBC=![]() ΓΝ(t+4t2+6t4)ΓΝ5ΘΫ15Θ§
ΓΝ(t+4t2+6t4)ΓΝ5ΘΫ15Θ§
ΫβΒΟt=2Μρt=3Θ§Β±t=2 ±Θ§y=-4
Β±t=3 ±Θ§y=-5Θ§
ΓύΒψPΉχ±ξΈΣΘ®2Θ§-4Θ©ΜρΘ®3Θ§-5Θ©ΘΜ
ΔΎΒ±ΒψPΈΣΘ®2Θ§-4Θ© ±Θ§
ΓΏ÷±œΏBCΫβΈω ΫΈΣΘΚy=-x+4Θ§QPΓΈBCΘ§
…η÷±œΏQPΒΡΫβΈω ΫΈΣΘΚy=-x+nΘ§
ΫΪΒψP¥ζ»κΘ§ΒΟ-4=-2+nΘ§n=-2Θ§
Γύ÷±œΏQPΒΡΫβΈω ΫΈΣΘΚy=-x-2Θ§
ΓύFΘ®0Θ§-2Θ©Θ§ΓœGOR=45ΓψΘ§
ΓύGB+![]() GF=GB+GR
GF=GB+GR
Β±G”ΎF÷ΊΚœ ±Θ§GB+GRΉν–ΓΘ§¥Υ ±ΒψGΒΡΉχ±ξΈΣΘ®0Θ§-2Θ©Θ§
Ά§άμΘ§Β±ΒψPΈΣΘ®3Θ§-5Θ© ±Θ§÷±œΏQPΒΡΫβΈω ΫΈΣΘΚy=-x-2Θ§
Ά§άμΩ…ΒΟΒψGΒΡΉχ±ξΈΣΘ®0Θ§-2Θ©Θ§
(3) Θ©ΓΏAΘ®1Θ§-1Θ©Θ§BΘ®5Θ§-1Θ©CΘ®0Θ§4Θ©Θ§
ΓύAC=![]() Θ§BC=5
Θ§BC=5![]() Θ§
Θ§
ΓΏSΓςABC=![]() ACΓΝBCsinΓœACBΘΫ
ACΓΝBCsinΓœACBΘΫ![]() ABΓΝ5Θ§
ABΓΝ5Θ§
ΓύsinΓœACB=![]() Θ§tanΓœACB=
Θ§tanΓœACB=![]() Θ§
Θ§
ΓΏAEΈΣ÷±ΨΕΘ§AB=4Θ§
ΓύΓœABE=90ΓψΘ§
ΓΏsinΓœAEB=sinΓœACB=![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύAE=2![]() Θ§
Θ§
ΓΏMBΓΆNBΘ§ΓœNMB=ΓœEABΘ§
ΓύΓœN=ΓœAEB=ΓœACBΘ§
ΓύtanN=![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύBN=![]() MBΘ§
MBȧ
Β±MBΈΣ÷±ΨΕ ±Θ§BNΒΡ≥ΛΕ»Ήν¥σΘ§ΈΣ3![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ