题目内容
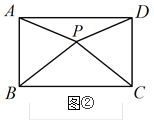
【题目】如图,矩形ABCD的对角线AC和BD相交于点O,DE平分∠ADC,若∠BDE=15°,则∠OEC 的度数为_________
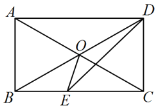
【答案】75°
【解析】
根据角平分线的定义和已知求出∠CDE =45°,∠ODC=60°,结合矩形的性质可得△EDC为等腰直角三角形,△OCD为等边三角形,由OC=EC利用三角形内角和定理求解即可.
解:在矩形ABCD中,DE平分∠ADC,∠BDE=15°,
∴∠ADE=∠CDE=![]() ∠ADC=45°,
∠ADC=45°,
∴∠ODC=15°+45°=60°,△EDC为等腰直角三角形,
∵OC=OD,
∴△OCD为等边三角形,
∴OC=CD,CD=EC,
∴OC=EC,
∵∠OCE=90°-60°=30°,
∴∠OEC=∠EOC=(180°-30°)÷2=75°,
故答案为:75°.

练习册系列答案
相关题目
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
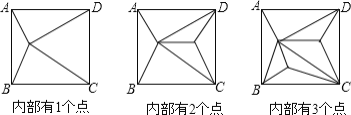
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.