题目内容
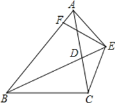
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
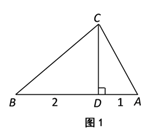
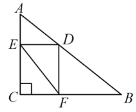
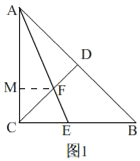
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
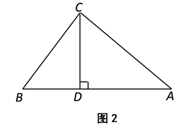
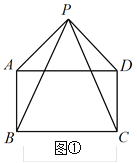
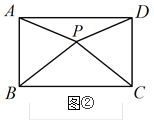
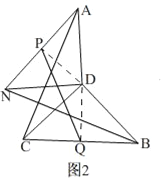
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=![]() PQ;
PQ;
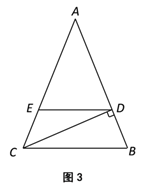
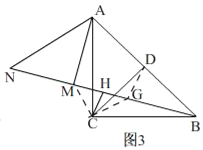
(3)如图3,将△ADC绕点A顺时针旋转一定角度到△AMN,其中D的对应点是M,C的对应点是N,若B,M,N三点在同一直线上,H为BN中点,连接CH,猜想BM,MN,CH之间的数量关系,请直接写出结果.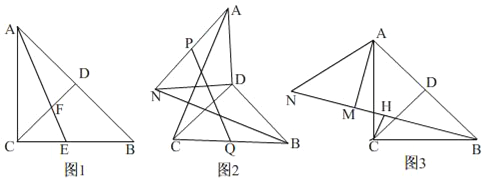
【答案】(1)AC=4+2![]() ;(2)见解析;(3)BM﹣MN=2CH,理由见解析
;(2)见解析;(3)BM﹣MN=2CH,理由见解析
【解析】(1)利用角平分线定理求出FM,再利用等腰直角三角形的性质即可得出CF,最后用AC=![]() CD即可;
CD即可;
(2)先判断出DN:DP=DB:DQ=![]() ,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
(3)先判断出,∠MAC=∠GBC进而得出△ACM≌△BCG,即可得出∠ACM=∠BCG,进而△MCG是直角三角形,再用直角三角形的中线得出MG=2CH,最后等量代换即可.
(1)如图1∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∴CD⊥AB,∠ACD=45°
过点F作FM⊥AC,
∵AE平分∠CAB,
∴FM=FD=2
在Rt△CMF中,∠ACD=45°,
∴CF=![]() MF=2
MF=2![]() ,
,
∴CD=CF+FD=2![]() +2,
+2,
∵CD是等腰直角三角形斜边的中线,
∴AC=![]() CD=
CD=![]() (2
(2![]() +2)=4+2
+2)=4+2![]() ;
;
(2)如图2,连接DP,DQ,
∵△ADC绕点D顺时针旋转一定角度得到△ADN,
∴AN=BC,DN=CD=DB,△ADN是等腰直角三角形,
∵△BCD是等腰直角三角形,点Q是BC中点,
∴DQ=![]() BC=
BC=![]() ×
×![]() BD=
BD=![]() DN,
DN,
∵点P是AN中点,
∴DP=![]() AN=
AN=![]() BC=DQ,
BC=DQ,
∴![]() =
=![]() ,
,
∵∠NDP=∠CDQ=45°,
∴∠PDQ=∠PDN+∠CDN+∠CDQ=90°+∠CDN,
∵∠NDB=∠CDN+∠CDB=90°+∠CDN,
∴∠PDQ=∠NDB,
∵![]() =
=![]() ,
,
∴△PDQ∽△NDB,
∴![]() =
=![]() ,
,
∴BN=![]() PQ.
PQ.
(3)BM﹣MN=2CH.
理由:如图3,在BN上截取BG=BD,连接CG,CM,
∵△ADC绕点A顺时针旋转一定角度到△AMN,
∴MN=AM=AD=CD=DB,
∴MN=AM=BG,
根据三角形的内角和,得∠MAC=∠GBC,
在△ACM和△BCG中,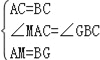 ,
,
∴△ACM≌△BCG,
∴∠ACM=∠BCG,
∴∠MCG=∠ACM+∠ACG=∠BCG+∠ACG=90°,
∴△MCG是直角三角形,
∵H为BN中点,
∴BH=NH,
∵BG=MN,
∴HG=HM,
在Rt△MCG中,HG=HM,
∴MG=2CH,
∴BM=BG+MG=MN+2CH,
∴BM﹣MN=2CH.

【题目】电影《我和我的祖国》讲述了新中国成立70年间普通百姓与共和国息息相关的故事.影片上映15天就斩获票房26亿元人民币,口碑票房实现双丰收.据统计,10月8日,该电影在重庆的票房收入为140万元,接下来7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房):
日期 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
票房变化(万元) |
|
| 0 |
|
|
|
|
(1)这7天中,票房收入最多的是10月________日,票房收入最少的是10月________日;
(2)根据上述数据可知,这7天该电影在重庆的平均票房收入为多少万元?