题目内容
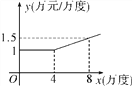
【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
【答案】(1);(2) z= ;(3)工厂最大月效益为54万元.
;(3)工厂最大月效益为54万元.
【解析】分析:(1)根据题意,电价y与用电量x的函数关系式是分段函数,当0≤x≤4时y=1,当4<x≤16时待定系数法可求得,(2)根据效益=产值-用电量×电价,分0≤x≤4,4<x≤16两种情况分别表示可得,(3)根据一次函数和二次函数性质结合自变量取值范围得到最大值,比较即可.
详解:(1)由题图知电价y与用电量x的函数关系式是分段函数.
当0≤x≤4时,y=1,
当4<x≤16时,函数是过点(4,1)和(8,1.5)的一次函数,
设一次函数为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴电价y与用电量x的函数关系为
y= ,
,
(2)月效益z与用电量x之间的函数关系式为:
z= ,
,
即z= ,
,
(3)当0≤x≤4时,z=![]() x,此时,z随着x的增大而增大,
x,此时,z随着x的增大而增大,
∴当x=4时,z取最大值为18.
当4<x≤16时,z=-![]() x2+
x2+![]() x-2=-
x-2=-![]() (x-22)2+
(x-22)2+![]() ,
,
∴当x≤22时,z随x的增大而增大,
∴当x=16时,z取最大值为54.
故当0≤x≤16时,z的最大值为54,
即工厂最大月效益为54万元.

练习册系列答案
相关题目