Question

【题目】在△ABC中，∠BAC=90°，AB=AC，l是过A的一条直线，BD⊥AE于D，CE⊥AE于E．求证：

（1）当直线l绕点A旋转到如图1位置时，试说明：DE=BD+CE．

（2）若直线l绕点A旋转到如图2位置时，试说明：DE=BD﹣CE．

（3）若直线l绕点A旋转到如图3位置时，试问：BD与DE，CE具有怎样的等量关系？请写出结果，不必证明．

Answer 1

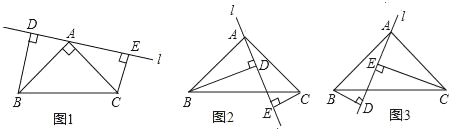
【答案】（1）证明见解析（2）证明见解析（3）DE=CE﹣BD

【解析】

(1) 利用条件证明△ABD≌△CAE, 再结合线段的和差可得出结论;

(2) 同 (1) 可证明△ABD≌△CAE, 再结合线段的和差可得出结论;

(3) 同理可证明△ABD≌△CAE, 再结合线段的和差可得出结论.

（1）证明：如图1，∵BD⊥l，CE⊥l，

∴∠BDA=∠CEA=90°，

∴∠ABD+∠DAB=90°．

∵∠BAC=90°，

∴∠DAB+∠CAE=90°，

∴∠ABD=∠CAE．

在△ABD和△CAE中，

，

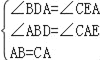∴△ABD≌△CAE（AAS），

∴AD=CE，BD=AE．

∵DE=AD+AE，

∴DE=CE+BD；

（2）如图2，∵BD⊥l，CE⊥l，

∴∠BDA=∠CEA=90°，

∴∠ABD+∠DAB=90°．

∵∠BAC=90°，

∴∠DAB+∠CAE=90°，∴∠ABD=∠CAE．

在△ABD和△CAE中，

，

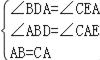∴△ABD≌△CAE（AAS），

∴AD=CE，BD=AE

∵DE=AE﹣AD，

∴DE=BD﹣CE．

（3）DE=CE﹣BD

如图3，∵BD⊥l，CE⊥l，

∴∠BDA=∠CEA=90°，

∴∠ABD+∠DAB=90°．

∵∠BAC=90°，

∴∠DAB+∠CAE=90°，

∴∠ABD=∠CAE．

在△ABD和△CAE中，

，

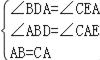∴△ABD≌△CAE（AAS），

∴AD=CE，BD=AE

∵DE=AD﹣AE，

∴DE=CE﹣BD．