题目内容
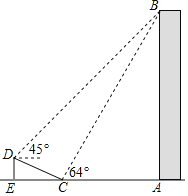
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
【答案】(1)斜坡CD的高度DE是5米;(2)大楼AB的高度是34米.
【解析】试题分析:(1)根据在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1: ![]() ,高为DE,可以求得DE的高度;
,高为DE,可以求得DE的高度;
(2)根据锐角三角函数和题目中的数据可以求得大楼AB的高度.
试题解析:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1: ![]() ,
,
∴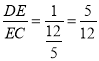 ,
,
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得:x=1,
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米;
(2)过点D作AB的垂线,垂足为H,设DH的长为x,
由题意可知∠BDH=45°,
∴BH=DH=x,DE=5,
在直角三角形CDE中,根据勾股定理可求CE=12,AB=x+5,AC=x-12,
∵tan64°=![]() ,
,
∴2=![]() ,
,
解得,x=29,AB=x+5=34,
即大楼AB的高度是34米.

练习册系列答案
相关题目