题目内容
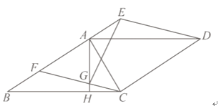
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E, DF∥AB交BC于点F .
(1)求证:四边形BEDF是菱形
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.

【答案】(1)见详解;(2)35°
【解析】
(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;
(2)由三角形内角和定理求出∠ABC=70°,由菱形的性质即可得出答案.
(1)证明:∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF=![]() ∠ABC
∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°-80°-30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,∠BDE=![]() ∠EDF=35°.
∠EDF=35°.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目