题目内容
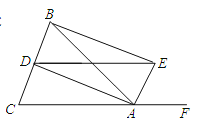
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF

(1)求∠CDE的度数
(2)求证:DF是⊙O的切线
【答案】证明见解析
【解析】试题分析:(1)直接利用圆周角定理得出∠CDE的度数;
(2)直接利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,进而得出答案.
试题解析:(1)∵对角线AC为⊙O的直径,
∴∠ADC=90°,
∴∠EDC=90°;
(2)连接DO,
∵∠EDC=90°,F是EC的中点,∴DF=FC,
∴∠FDC=∠FCD,
∵OD=OC ,∴∠OCD=∠ODC,
∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是⊙O的切线.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目