题目内容
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
【答案】(1) 甲种材料每千克25元,乙种材料每千克35元;(2) 有三种方案;(3) 生产![]() 产品22件,
产品22件,![]() 产品38件成本最低
产品38件成本最低
【解析】
(1)设甲材料每千克x元,乙材料每千克y元,根据购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元,可列出方程组
![]() ,解方程组即可得到甲材料每千克25元,乙材料每千克35元;
,解方程组即可得到甲材料每千克25元,乙材料每千克35元;
(2)设生产A产品m件,生产B产品(60-m)件,先表示出生产这60件产品的材料费为25×4m+35×1m+25×3(60-m)+35×3(60-m)=-45m+10800,根据购买甲、乙两种材料的资金不超过9900元得到-45m+10800≤9900,根据生产B产品不少于38件得到60-m≥38,然后解两个不等式求出其公共部分得到20≤m≤22,而m为整数,则m的值为20,21,22,易得符合条件的生产方案;
(3)设总生产成本为W元,加工费为:40m+50(60-m),根据成本=材料费+加工费得到W=-45m+10800+40m+50(60-m)=-55m+13800,根据一次函数的性质得到W随m的增大而减小,然后把m=22代入,即可得到最低成本的生产方案.
(1)设甲种材料每千克![]() 元,乙种材料每千克
元,乙种材料每千克![]() 元,依题意得:
元,依题意得:
![]() 解得
解得![]()
答:甲种材料每千克25元,乙种材料每千克35元.
(2)生产![]() 产品
产品![]() 件,生产
件,生产![]() 产品
产品![]() 件.依题意得:
件.依题意得:
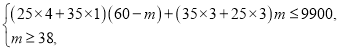
解得![]() .
.
![]()
![]() 的值为整数,
的值为整数,
![]() 的值为38,39,40.
的值为38,39,40.
![]() 共有三种方案:
共有三种方案:
| 22 | 21 | 20 |
| 38 | 39 | 40 |
(3)设生产成本为![]() 元,则
元,则
![]() ,
,
![]() ,
,![]() 随
随![]() 的增大而增大.
的增大而增大.
![]() 当
当![]() 时,总成本最低.
时,总成本最低.
答:生产![]() 产品22件,
产品22件,![]() 产品38件成本最低.
产品38件成本最低.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
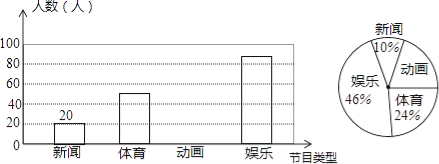
金牌课堂练系列答案【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
级别 | 家庭的文化教育消费金额 | 户数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
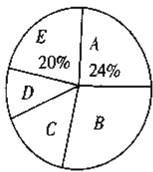
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有___________户,表中![]() ___________;
___________;
(2)在扇形统计图中,![]() 组所在扇形的圆心角为多少度?
组所在扇形的圆心角为多少度?
(3)这个社区有![]() 户家庭,请你估计年文化教育消费在
户家庭,请你估计年文化教育消费在![]() 元以上的家庭有多少户.
元以上的家庭有多少户.