题目内容
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 
【答案】2+2 ![]()
【解析】解:如图所示, 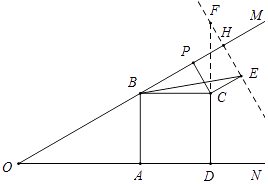
将BC绕着点C顺时针旋转90°得FC,作直线FE交OM于H,则∠BCF=90°,BC=FC,
∵将CP绕点C按顺时针方向旋转90°得CE,
∴∠PCE=90°,PC=EC,
∴∠BCP=∠FCE,
在△BCP和△FCE中, ,
,
∴△BCP≌△FCE(SAS),
∴∠CBP=∠CFE,
又∵∠BCF=90°,
∴∠BHF=90°,
∴点E在直线FH上,即点E的轨迹为直线FH,
∵BH⊥EF,
∴当点E与点H重合时,BE=BH最短,
∵当CP⊥OM时,Rt△BCP中,∠CBP=30°,
∴CP= ![]() BC=2,BP=
BC=2,BP= ![]() CP=2
CP=2 ![]() ,
,
又∵∠PCE=∠CPH=∠PHE=90°,CP=CE,
∴正方形CPHE中,PH=CP=2,
∴BH=BP+PH=2 ![]() +2,
+2,
即BE的最小值为2 ![]() +2,
+2,
故答案为:2 ![]() +2.
+2.
先将BC绕着点C顺时针旋转90°得FC,作直线FE交OM于H,则∠BCF=90°,BC=FC,根据旋转的性质,即可得到△BCP≌△FCE(SAS),进而得出∠BHF=90°,据此可得点E在直线FH上,即点E的轨迹为直线FH,再根据当点E与点H重合时,BE=BH最短,求得BH的值即可得到BE的最小值.

【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?