题目内容
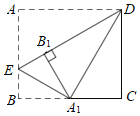
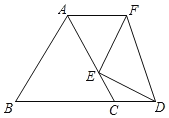
【题目】如图,△ABC是等边三角形,AB=3,点E在AC上,AE![]() AC,D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE,当AF∥BD时,线段AF的长为____.
AC,D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE,当AF∥BD时,线段AF的长为____.
【答案】1![]() .
.
【解析】
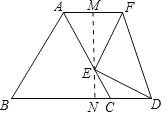
过点E作EM⊥AF于M,交BD于N,根据30°直角三角形的性质求出AM =1,再根据∠60°的三角函数值求出EN的长,再依据△EMF≌△DNE(AAS)得出MF=EN![]() ,据此可得,当AF∥BD时,线段AF的长为1
,据此可得,当AF∥BD时,线段AF的长为1![]() .
.
如图过点E作EM⊥AF于M,交BD于N.
∵△ABC是等边三角形,
∴AB=BC=AC=3,∠ACB=60°.
∵AE![]() AC,
AC,
∴AE=2,EC=1.
∵AF∥BD,
∴∠EAM=∠ACB=60°.
∵EM⊥AF,
∴∠AME=90°,
∴∠AEM=30°,
∴AM![]() AE=1.
AE=1.
∵AF∥BD,EM⊥AF,
∴EN⊥BC,
∴EN=ECsin60°![]() ,
,
∵∠EMF=∠END=∠FED=90°,
∴∠MEF+∠MFE=90°,∠MEF+∠DEN=90°,
∴∠EFM=∠DEN.
∵ED=EF,
∴△EMF≌△DNE(AAS),
∴MF=EN![]() ,
,
∴AF=AM+MF=1![]() .
.
故答案为:1![]() .
.

练习册系列答案
相关题目
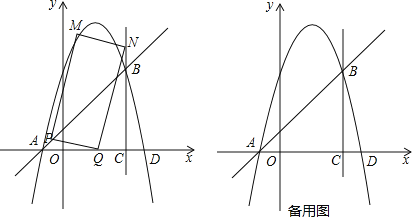
【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
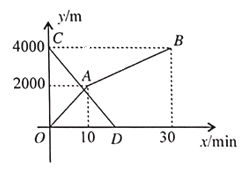
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
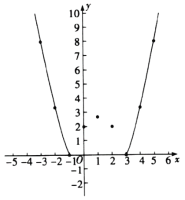
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程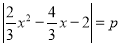 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.