题目内容
【题目】如图,已知四边形BCDE为平行四边形,点A在BE的延长线上且AE=EB.连接EC,AC,AD.
(1)求证:△AED≌△EBC.
(2)若∠ACB=90°,则四边形AECD是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵四边形BCDE是平行四边形,
∴ED∥BC,DE=BC,
∴∠AED=∠B,
在△AED和△EBC中,
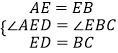 ,
,
∴△AED≌△EBC
(2)解:结论:四边形AECD是菱形.
理由:∵四边形BCDE是平行四边形,
∴AB∥CD,BE=CD,
∵AE=BE,
∴AE=CD,AE∥CD,
∴四边形AECD是平行四边形,
∵∠ACB=90°,
∴AC⊥BC,∵BC∥DE,
∴AC⊥DE,
∴四边形AECD是菱形.
【解析】(1)根据平行四边形的性质得出ED∥BC,DE=BC,进而得出∠AED=∠B,然后利用SAS判断出△AED≌△EBC;
(2)结论:四边形AECD是菱形.利用平行四边形的性质得出AB∥CD,BE=CD,进而判断出四边形AECD是平行四边形,然后根据平行线的性质得出AC⊥DE,从而得出四边形AECD是菱形.
【考点精析】本题主要考查了平行线的性质和平行四边形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂甲、乙两名工人参加操作技能培训.他们在培训期间参加的8次测试成绩记录如下表:
甲 | 73 | 82 | 70 | 85 | 80 | 70 | 75 | 65 |
乙 | 85 | 72 | 78 | 71 | 83 | 69 | 74 | 68 |
则下列说法错误的是( )
A.甲、乙的平均成绩都是75
B.甲成绩的众数是70
C.乙成绩的中位数是73
D.若从中选派一人参加操作技能比赛,从成绩稳定性考虑,应选甲