题目内容
【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
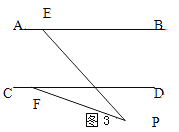
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
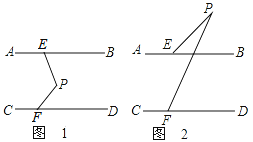
【答案】(1) ∠EPF=∠PEB+∠PFD; (2) ∠PFD=∠PEB+∠EPF;∠PEB=∠PFD+∠EPF.
【解析】
(1)过点P作PH∥AB∥CD,根据平行线的性质:两直线平行,内错角相等即可证得;(2)若点P在直线AB上方时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得;若点P在直线AB下方时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得.
解:(1)∠PEB,∠PFD,∠P满足的数量关系是∠EPF=∠PEB+∠PFD;
理由如下:如图1,过点P作PH∥AB∥CD
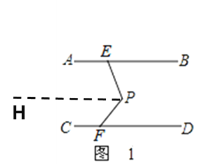
∴∠PEB=∠EPH,∠PFD=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠PEB+∠PFD;
(2)如图2,若点P在直线AB上方时,
∠PEB,∠PFD,∠P满足的数量关系是∠PFD=∠PFB+∠EPF;
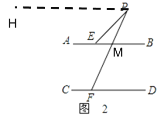
理由:过点P作PH∥AB∥CD
∴∠FPH=∠PFD=∠PMB
而∠PMB=∠PFB+∠EPF∴∠PFD=∠PFB+∠EPF;
如图3,若点P在直线AB下方时,
∠PEB,∠PFD,∠P满足的数量关系是∠PEB=∠PFD+∠EPF;
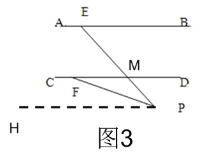
理由: 过点P作PH∥AB∥CD
∴∠PEB=∠EPH=∠DMP,而∠DMP=∠PFD+∠EPF.
∴∠PEB=∠PFD+∠EPF;

练习册系列答案
相关题目