Question

【题目】已知射线OM，ON，∠MON=45°点A在射线OM上，点B在射线ON上，OA=1，若△AOB是轴对称图形，点P为AB的中点，则OP2= ．

Answer 1

【答案】 或 或
【解析】解：如图所示，

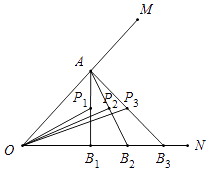
分三种情况：

①当AB1=OB1时，△AOB1是等腰直角三角形，AB1=OB1= ，

∴B1P1= AB1= × = ，

∴Rt△OB1P1中，OP12=OB12+B1P12=（ ）2+（ ）2= ；

②当AO=B2O时，△AOB2是等腰三角形，

Rt△AB1B2中，AB2= = ，

∵OP2⊥AB2，AB1⊥OB2，

∴ ×AB2×OP2= ×OB2×AB1，

∴OP2= = ，

∴OP22=（ ）2= ；

③当AO=AB3时，△AOB3是等腰直角三角形，

∵AP3= AB3= ，

∴Rt△AOP3中，OP32=AO2+AP32=12+（ ）2= ；

综上所述，OP2= 或 或 ．

所以答案是： 或 或 ．

【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握轴对称图形(两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴)的相关知识才是答题的关键．