题目内容
【题目】在菱形ABCD中,对角线AC、BD交于点O,且AC=16cm,BD=12cm;点P从点A出发,沿AD方向匀速运动,速度为2cm/s;点Q从点C出发,沿CO方向匀速运动,速度为1cm/s;若P、Q两点同时出发,当一个点停止运动时,另一个点也停止运动.过点Q作MQ∥BC,交BD于点M,设运动时间为t(s)(0<t<5).解答下列问题:
(1)求t为何值时,线段AQ、线段PM互相平分.
(2)设四边形APQM的面积为Scm2 , 求S关于t的函数关系式;设菱形ABCD的面积为SABCD , 求是否存在一个时刻t,使S:SABCD=2:5?如果存在,求出t,如果不存在,请说明理由.
(3)求时刻t,使得以M、P、Q为顶点的三角形是直角三角形.
【答案】
(1)解:如图1中,连接PM.

∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=8,OB=OD=6,AB∥BC,
∵QM∥BC,
∴AP∥QM,
当PA=QM时,四边形AMQP是平行四边形,此时AQ与PM互相平分.
在Rt△BOC中,BC= ![]() =10,
=10,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QM= ![]() (8﹣t),
(8﹣t),
∵PA=QM,
∴2t= ![]() (8﹣t),
(8﹣t),
∴t= ![]() ,
,
∴当t= ![]() 时,AQ与PM相互平分
时,AQ与PM相互平分
(2)解:不存在.理由如下:
如图2中,作QH⊥AD于H,

∵△AOD∽△AHQ,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QH= ![]() (16﹣t),
(16﹣t),
∴S= ![]() [2t+
[2t+ ![]() (8﹣t)]
(8﹣t)] ![]() (16﹣t)=﹣
(16﹣t)=﹣ ![]() t2+
t2+ ![]() t+48,
t+48,
∵S:SABCD=2:5,
∴ ![]() [2t+
[2t+ ![]() (8﹣t)]
(8﹣t)] ![]() (16﹣t):
(16﹣t): ![]() ×16×12=2:5,
×16×12=2:5,
整理得3t2﹣8t﹣128=0
∴t=8或﹣ ![]() ,
,
∵0<t<5,
∴t=8或﹣ ![]() 都不符合题意
都不符合题意
(3)解:①如图3中,当∠PMQ=90°时,
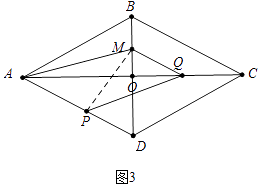
∵△MPD∽△AOD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() .
.
②如图4中,当PQ⊥MQ时,
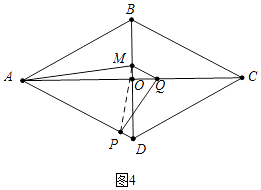
∵△APQ∽△AOD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
综上所述,当t= ![]() s或
s或 ![]() s时,△PQM是直角三角形
s时,△PQM是直角三角形
【解析】(1)当AP=QM时,列出方程即可解决问题;
(2)不存在.理由如下:如图2中,作QH⊥AD于H,由△AOD∽△AHQ,可得![]() =
=![]() ,L列出关于t的方程,根据梯形的面积公式计算即可;
,L列出关于t的方程,根据梯形的面积公式计算即可;
(3)分两种情形①如图3中,当∠PMQ=90°时,②如图4中,当PQ⊥MQ时,分别利用相似三角形的性质,列出方程即可解决问题。
【考点精析】通过灵活运用勾股定理的概念和梯形的定义,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形即可以解答此题.

 口算能手系列答案
口算能手系列答案【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.