Question

【题目】如图，甲船在港口P的南偏西60°方向，距港口80海里的A处，沿AP方向以每小时18海里的速度匀速驶向港口P．乙船从港口P出发，沿南偏东45°方向匀速驶离港口P，已知两船同时出发，经过2小时乙船恰好在甲船的正东方向．求乙船的行驶速度．（结果保留根号）

Answer 1

【答案】乙船的航行速度约为每小时11海里．

【解析】

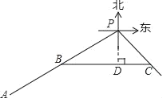
设乙船的航行速度为每小时x海里，2小时后甲船在点B处，乙船在点C处，则PC＝2x海里，过P作PD⊥BC于D，求出BP，在Rt△BPD中求出PD，然后在Rt△PDC中表示出PD，继而建立方程可解出x的值．

设乙船的航行速度为每小时x海里，2小时后甲船在点B处，乙船在点C处，则PC＝2x海里，

过P作PD⊥BC于D，则BP＝80﹣2×18＝44（海里），

在Rt△PDB中，∠PDB＝90°，∠BPD＝60°，

∴PD＝PBcos60°＝22（海里），

在Rt△PDC中，∠PDC＝90°，∠DPC＝45°，

∴PD＝PCcos45°＝2x＝x，

∴x＝22，即x＝11，

答：乙船的航行速度约为每小时11海里．