题目内容
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
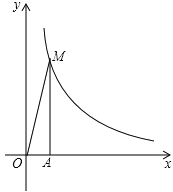
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
【答案】(1)![]() (2)7或3.
(2)7或3.
【解析】试题分析:(1)根据反比例函数k的几何意义得到![]() |k|=3,可得到满足条件的k=6,于是得到反比例函数解析式为y=
|k|=3,可得到满足条件的k=6,于是得到反比例函数解析式为y=![]() ;
;
(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数y=![]() 的图象上,则D点与M点重合,即AB=AM,再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数y=
的图象上,则D点与M点重合,即AB=AM,再利用反比例函数图象上点的坐标特征确定M点坐标为(1,6),则AB=AM=6,所以t=1+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数y=![]() 的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t,t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.
的图象上,根据正方形的性质得AB=BC=t-1,则C点坐标为(t,t-1),然后利用反比例函数图象上点的坐标特征得到t(t-1)=6,再解方程得到满足条件的t的值.
试题解析:(1)∵△AOM的面积为3,
∴![]() |k|=3,
|k|=3,
而k>0,
∴k=6,
∴反比例函数解析式为y=![]() ;
;
(2)当以AB为一边的正方形ABCD的顶点D在反比例函数y=![]() 的图象上,则D点与M点重合,即AB=AM,
的图象上,则D点与M点重合,即AB=AM,
把x=1代入y=![]() 得y=6,
得y=6,
∴M点坐标为(1,6),
∴AB=AM=6,
∴t=1+6=7;
当以AB为一边的正方形ABCD的顶点C在反比例函数y=![]() 的图象上,
的图象上,
则AB=BC=t-1,
∴C点坐标为(t,t-1),
∴t(t-1)=6,
整理为t2-t-6=0,解得t1=3,t2=-2(舍去),
∴t=3,
∴以AB为一边的正方形有一个顶点在反比例函数y=![]() 的图象上时,t的值为7或3.
的图象上时,t的值为7或3.

练习册系列答案
相关题目