Question

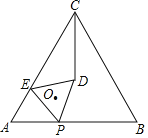
【题目】如图，已知等边△ABC的边长为4，P是AB边上的一个动点，连接CP，过点P作∠EPC＝60°，交AC于点E，以PE为边作等边△EPD，顶点D在线段PC上，O是△EPD的外心，当点P从点A运动到点B的过程中，点O也随之运动，则点O经过的路径长为_____．

Answer 1

【答案】

【解析】

根据等边三角形的外心性质，根据特殊角的三角函数即可求解．

解：如图，作BG⊥AC、CF⊥AB于点G、F，交于点I，

则点I是等边三角形ABC的外心，

∵等边三角形ABC的边长为4，

∴AF＝BF＝2

∠IAF＝30°

∴AI＝

∵点P是AB边上的一个动点，O是等边三角形△EPD的外心，

∴当点P从点A运动到点B的过程中，点O也随之运动，

点O的经过的路径长是AI的长，

∴点O的经过的路径长是．

故答案为：．