题目内容
【题目】如图,在△ABC中,∠A=90°,以AB为直径的O交BC于D,点E为AC的中点,连接DE.
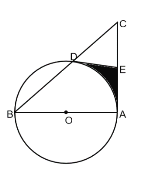
(1)求证:DE是O的切线;
(2)若∠BAD=50°,AC=6,CD=4,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OD,DA,利用直角三角形的性质证明![]() ,利用等腰三角形的性质可得结论;
,利用等腰三角形的性质可得结论;
(2)证明△ADC∽△BAC,求解圆的半径,利用S阴影=S四边形OAED-S扇形AOD可得答案.
解:(1)连接OD,DA
∵AB是O的直径,
∴∠BDA=∠CDA=90°
∵点E是AC的中点
∴在Rt△ACD中,DE=AE,
∴∠EDA=∠DAE
∵OD=OA
∴∠OAD=∠ODA
又∵∠BAC=90°
∴∠EDA+∠ODA=∠DAE+∠OAD=90°
即∠ODE=90°
∴OD⊥DE
又∵点D在O上
∴DE是O的切线·

(2)由题知∠ADC=∠BAC=90°,∠C=∠C
∴△ADC∽△BAC
∴![]() ,即
,即![]()
∴BC=9
在Rt△ABC中,由勾股定理可得AB=![]()
∴OA=![]() ,
,
连接![]()
![]()
![]() S四边形OAED
S四边形OAED![]()
∵OA=OD,DE=AE=3
∴S四边形OAED ![]()
又∵弧BD所对圆周角为50°
∴∠BOD=100°,则∠AOD=80°
∴S扇形AOD 
∴S阴影=S四边形OAED-S扇形AOD![]()


 阅读快车系列答案
阅读快车系列答案【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:
80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
|
| 5 |
|
|
|
|
|
|
|
| 2 |
八、九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 |
|
|
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)八年级王宇和九年级程义的分数都为80分,请判断王宇、程义在各自年级的排名哪位更靠前?请简述你的理由;
(3)八年级被抽取的20名学生中,获得![]() 等和
等和![]() 等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为
等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为![]() 等的概率.
等的概率.