题目内容
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如图所示的统计图:
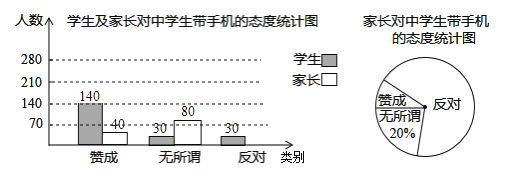
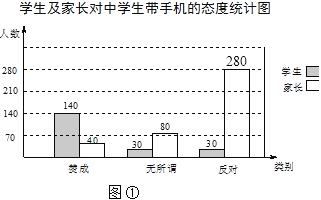
(1)求这次调查的家长人数,并补全图①:
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
(4)为更深入的了解学生的看法,又从“赞成”的学生甲、乙、丙、丁四人中随机选取2人,请用树状图法或列表法求出恰好选中甲和乙的概率.
【答案】(1)400,详见解析;(2)36°;(3)0.15;(4)![]()
【解析】
(1)由扇形统计图可知,家长“无所谓”占20%,从条形统计图可知,“无所谓”有80人,即可求出这次调查的家长人数;
(2)在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比,赞成的有40人,则圆心角的度数可求;
(3)用学生“无所谓”30人,除以学生赞成、无所谓、反对总人数即可求得其概率.
(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式求解即可求得答案.
解:(1)家长人数为80÷20%=400,
补全图①如下:
(2)表示家长“赞成”的圆心角的度数为![]() ;
;
(3)学生恰好持“无所谓”态度的概率是![]() .
.
(4)画树状图得:
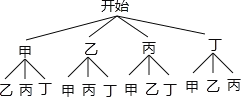
∵所有出现的等可能性结果共有12种,其中满足条件的结果有2种.
∴P(恰好选中甲、乙两位同学)=![]() .
.

练习册系列答案
相关题目