题目内容
【题目】为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本![]() (元)与月份
(元)与月份![]() (月)之间的关系可近似地表示为:
(月)之间的关系可近似地表示为:![]() ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为![]() (吨),每月的利润为
(吨),每月的利润为![]() (元).
(元).
(1)分别求出![]() 与
与![]() ,
,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)在今年内该单位哪个月获得利润达到5800元?
【答案】(1)![]() ,
,![]() ;(2)在今年内该单位5月份获得利润达到5800元
;(2)在今年内该单位5月份获得利润达到5800元
【解析】
(1)根据“该单位每月再生资源处理量每一个月将提高10吨”即可求出y与x的函数关系式,然后根据“利润=售价-成本”即可求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)将![]() =5800代入到(1)中关系式中,然后解一元二次方程即可求出结论.
=5800代入到(1)中关系式中,然后解一元二次方程即可求出结论.
解:(1)根据题意![]()
故每月再生资源处理量(吨)与月份之间的关系式为:![]() ,
,
![]() ;
;
(2)由题意可知:![]()
![]()
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
∴在今年内该单位5月份获得利润达到5800元.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
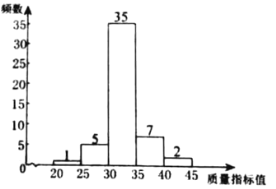
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)
【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
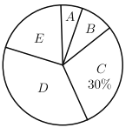
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3