题目内容
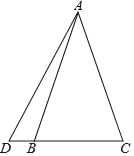
【题目】已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为_____.
【答案】2![]()
【解析】
作辅助线,构建正方形AHGF,则AF=GH=GF,设GC=x,则FG=AF=HG=x+2,DG=x-1,在Rt△DGC中,利用勾股定理列方程可求得x的值,最后利用勾股定理计算AC的长即可.
解:过A作AE⊥DC于E,将△AEC沿AC翻折得△AFC,将△ADE沿AD翻折得△ADH,延长FC、HD交于G,
则∠EAC=∠CAF,∠EAD=∠HAD,∠H=∠F=90°,
∴∠EAC+∠EAD=∠CAF+∠HAD,
∵∠DAC=45°,即∠EAC+∠EAD=45°,
∴∠HAF=90°,
∴四边形AHGF是矩形,
∵AH=AE,AE=AF,
∴AH=AF,
∴四边形AHGF是正方形,
∴AF=GH=GF,
∵AB=AC,AE⊥BC,
∴BE=EC=2,
由折叠得:FC=EC=2,HD=DE=3,
设GC=x,则FG=AF=HG=x+2,
∴DG=x-1,
在Rt△DGC中,DC2=DG2+GC2,
52=(x-1)2+x2,
解得:x1=4,x2=-3(舍),
∴AF=x+2=4+2=6,
Rt△ACF中,AC=2![]()
故答案为:2![]() .
.

练习册系列答案
相关题目