题目内容
【题目】在平面直角坐标系中，已知A，B，C，D四点的坐标依次为（0，0），（6，2），（8，8），（2，6），若一次函数y＝mx﹣6m+2（m≠0）图象将四边形ABCD的面积分成1：3两部分，则m的值为（ ）
A. ﹣4B. 
，﹣5C. D. 
，﹣4
【答案】B
【解析】
由题意直线y＝mx﹣6m+2经过定点B（6，2），又直线L把菱形ABCD的面积分成1：3的两部分．即可推出L经过AD的中点M（1，3）或经过CD的中点N（5，7），利用待定系数法即可解决问题．
如图：
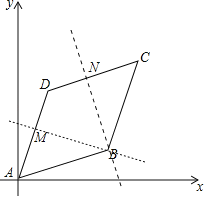
∵A、B、C、D四点的坐标依次为（0，0）、（6，2）、（8，8）、（2，6），
∴AB＝BC＝CD＝AD＝2
，
∴四边形ABCD是菱形，
∵直线y＝mx﹣6m+2经过定点B（6，2），
又∵直线L把菱形ABCD的面积分成1：3的两部分．
∴L经过AD的中点M（1，3）或经过CD的中点N（5，7），
∴m﹣6m+2＝3或5m﹣6m+2＝7，
∴m＝
或﹣5，
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
