Question

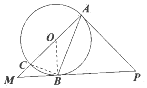
【题目】如图，AC是⊙O的直径，点B为⊙O上一点，PA切⊙O于点A，PB与AC的延长线交于点M，∠CAB＝ ∠APB．

（1）求证：PB是⊙O的切线；

（2）当sinM＝，OA＝2时，求MB，AB的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）连接OB，根据切线的性质得到OA⊥AP，求得∠OBM=90°，OB⊥MP，根据求得的判定定理即可得到结论；

（2）连接BC，解直角三角形得到MC=1，MB=，根据圆周角定理得到∠ABC=90°，根据相似三角形的性质得到AB=CB，根据勾股定理即可得到结论．

（1）证明：连接，

∵，∴

∵是的切线，∴，∴，

∴，∴，∴，且为半径，∴为的切线.

（2）连接，

∵，∴，∴，∴

∵为直径∴，∴，

∵，∴，

∵，∴，又∵，∴

∴，∴，又∵

即，

∴，

∴AB=.