题目内容
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )
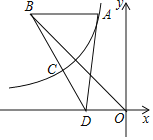
A. -![]() B. -3C. -2D.
B. -3C. -2D. ![]()
【答案】C
【解析】
如图作BH⊥OD于H.延长BA交y轴于E.由tan∠ABD=tan∠BDH=![]() ,设DH=5m,BH=9m,则BH=BE=9m,OD=4m,推出C(-6m,
,设DH=5m,BH=9m,则BH=BE=9m,OD=4m,推出C(-6m,![]() m),推出A(-
m),推出A(-![]() m,9m),由△ABD的面积为
m,9m),由△ABD的面积为![]() ,推出
,推出![]() m×9m=
m×9m=![]() ,可得m2=
,可得m2=![]() ,推出k=-6m×
,推出k=-6m×![]() m=-2;
m=-2;
如图,作BH⊥OD于H.延长BA交y轴于E.
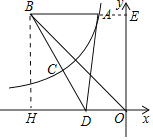
∵AB∥DH,
∴∠ABD=∠BDH,
∴tan∠ABD=tan∠BDH=![]() ,设DH=5m,BH=9m,则BH=BE=9m,OD=4m,
,设DH=5m,BH=9m,则BH=BE=9m,OD=4m,
∴C(-6m,![]() m),
m),
∴A(-![]() m,9m),
m,9m),
∵△ABD的面积为![]() ,
,
∴![]() m×9m=
m×9m=![]() ,
,
∴m2=![]() ,
,
∴k=-6m×![]() m=-2,
m=-2,
故选C.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目