题目内容
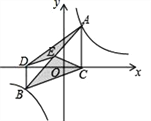
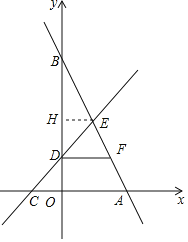
【题目】如图,直线![]() 分别与x轴、y轴交于点
分别与x轴、y轴交于点![]() 和点B,直线
和点B,直线![]() 分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为
分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为![]() 的中点。
的中点。
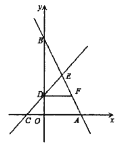
(1)求直线![]() 的解析式;
的解析式;
(2)过点D作![]() 轴,交直线
轴,交直线![]() 于点F,求
于点F,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)过E作EH⊥y轴于H,由y=x+1,求得D的坐标为(0,1)C(-1,0),再根据△COD≌△EHD,由全等三角形的性质得到EH=OC=1,DH=OD=1,即可求得E点的坐标,由待定系数法即可求得直线y=kx+b的解析式;
(2)根据三角形的中位线定理求得DF,由E(1,2),D的坐标为(0,1),求得E到DF的距离为1,根据三角形的面积公式即可求得结论.
(1)过E作EH⊥y轴于H,
把x=0代入y=x+1,得y=1,
∴D的坐标为(0,1),
∴OD=1,
把y=0代入y=x+1,得x=-1,
∴C(-1,0),
∵点D为CE的中点,
∴△COD≌△EHD,
∴EH=OC=1,DH=OD=1,
∴E(1,2),
把A,E点的坐标代入y=kx+b中,得![]() ,
,
解得![]() ,
,
∴直线y=kx+b的解析式为y=-2x+4;
(2)
∵A(2,0),
∴AC=3,
∵D为CE的中点,DF∥x轴,
∴F为EA的中点,
∴DF=![]() AC=
AC=![]() ,
,
∵E(1,2),D的坐标为(0,1),
∴E到DF的距离为1,
∴△DEF的面积=![]() ×
×![]() ×1=
×1=![]() .
.

练习册系列答案
相关题目