题目内容
【题目】(1)解方程: 3y(y﹣1)=2﹣2y
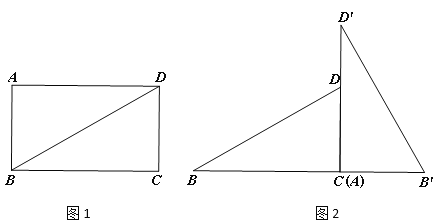
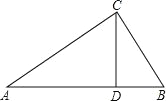
(2)如图,△ABC中,CD是边AB上的高,且![]() .求∠ACB的大小.
.求∠ACB的大小.
【答案】(1)![]() ,y2=1;(2) 90°.
,y2=1;(2) 90°.
【解析】试题分析:
(1)根据本题特点,用“因式分解法”解此方程即可;
(2)由△ABC中,CD是边AB上的高,可得∠ADC=∠CDB=90°,结合![]() 可证得:△ADC∽△CDB,从而可得∠BCD=∠A,结合∠A+∠ACD=90°可得∠BCD+∠ACD=∠ACB=90°.
可证得:△ADC∽△CDB,从而可得∠BCD=∠A,结合∠A+∠ACD=90°可得∠BCD+∠ACD=∠ACB=90°.
试题解析:
(1)方程整理得:3y(y-1)-2(y-1)=0,
分解因式得:(3y-2)(y-1)=0,
解得: ![]() ,y2=1.
,y2=1.
(2)∴∠ADC=∠BDC=90°;
又∵AD:CD=CD:BD,
∴△ADC∽△CDB;
∴∠ACD=∠B;
∵∠A+∠ACD=90°,
∴∠A+∠B=90°,即∠ACB=90°.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目