��Ŀ����
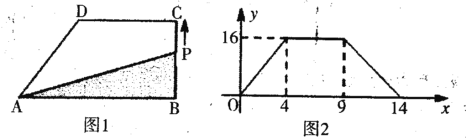
����Ŀ����ͼ���������ϵ�A��ʾ����a����B��ʾ��b��a��b����|a��40|+��b+8��2��0����O������ԭ�㣮
![]()
��1����A��ʾ����Ϊ ����B��ʾ����Ϊ ���߶�AB�ij�Ϊ ��
��2������A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��������������һ��C��ʹAC��2BC�����C�������ϱ�ʾ����Ϊ ��
��3�����ж���P��Q����B���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���O��ʱ����Q�Ŵ�B�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����Q��ֹͣ�ƶ������P�ƶ���ʱ��Ϊt�룬�ʣ���tΪ����ʱ��P��Q�������4����λ���ȣ�
���𰸡���1����A��ʾ����Ϊ40����B��ʾ����Ϊ��8���߶�AB�ij�Ϊ48����2��8��40��3����tΪ4�롢10���14��ʱ��P��Q�������4����λ����
��������
��1������ż�η��Լ�����ֵ�ķǸ��Լ������a��b��ֵ���ɵõ�A��ʾ��������B��ʾ�������ٸ��������ľ��빫ʽ�����߶�AB�ij���
��2���������������C���߶�AB�ϣ���C������AB�ϣ��������ۼ�����⣻
��3����0��t��8��8��t��12��12��t��48����������ǣ�����P��Q�ƶ���·�̽��PQ��4���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺��1����|a��40|+��b+8��2��0��
��a��40��0��b+8��0��
���a��40��b����8��
AB��40������8����48��
�ʵ�A��ʾ����Ϊ40����B��ʾ����Ϊ��8���߶�AB�ij�Ϊ48��
��2����C���߶�AB�ϣ�
��AC��2BC��
��AC��48��![]() ��32��
��32��
��C�������ϱ�ʾ����Ϊ40��32��8��
��C������AB�ϣ�
��AC��2BC��
��AC��40��2��80��
��C�������ϱ�ʾ����Ϊ40��80����40��
�ʵ�C�������ϱ�ʾ����Ϊ8��40��
��3����i����0��t��8ʱ����Q���ڵ�B����
��PQ��t��4��
��ii����8��t��12ʱ����P�ڵ�Q���Ҳ࣬
��![]()
��ã�![]() ��
��
��iii����12��t��48ʱ����P�ڵ�Q����࣬
��3��t��8����t��4��
��ã�t��14��
������������tΪ4�롢10���14��ʱ��P��Q�������4����λ���ȣ�

����Ŀ��ijͬѧ��ѧ�ڵ���ѧ���β���ɼ����±���ʾ��
������� | ƽʱ���� | ���в��� | ��ĩ���� | ||
��1�� | ��2�� | ��3�� | |||
�ɼ� | 100 | 106 | 106 | 105 | 110 |
��1����ͬѧ��ѧ��5�β���ɼ�������Ϊ ����λ��Ϊ ��
��2����ͬѧ��ѧ����ѧƽʱ�ɼ���ƽ����Ϊ ��
��3����ͬѧ��ѧ�ڵ��ܳɼ��ǽ�ƽʱ�����ƽ���ɼ������в���ɼ�����ĩ����ɼ�����2��3��5�ı����������ã����ͬѧ��ѧ����ѧѧ�Ƶ������ɼ������������������
����Ŀ��ijʳƷ���������Ĵ�װʳƷ�г����Ʒ20������ÿ��������45��Ϊ�������ÿ���������Ƿ���ϸñ�����������Ŀ����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ���ˣ� | ��5 | ��3 | 0 | 1 | 2 | 5 |
���� | 1 | 3 | 6 | 4 | 5 | 1 |
�ش��������⣺
��1����20����Ʒ�У���ȫ����ÿ��������45�˵����� ������
��2��������Ʒ���������Ƕ��ٿˣ���Ҫ��д����ʽ����