Question

【题目】如图，在Rt△ABC中，∠C=90°，点D在线段AB上，以AD为直径的⊙O与BC相交于点E，与AC相交于点F，∠B=∠BAE=30°．

（1）求证：BC是⊙O的切线；

（2）若AC=3，求⊙O的半径r；

（3）在（1）的条件下，判断以A、O、E、F为顶点的四边形为哪种特殊四边形，并说明理由．

Answer 1

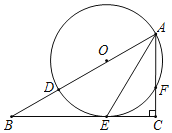
【答案】（1）证明见解析；（2）⊙O的半径为2；（3）四边形OAFE是菱形，理由见解析.

【解析】（1）利用等腰三角形的性质和三角形外角的性质得出∠AOE=60°，进而得出∠BEO=90°，即可得出结论；

（2）先求出∠AEC=60°，利用锐角三角函数求出AE，最后用三角函数即可得出结论；

（3）先判断出△AOF是等边三角形，得出OA=AF，∠AOF=60°，进而判断出△OEF是等边三角形，即可判断出四边相等，即可得出结论．

（1）如图1，

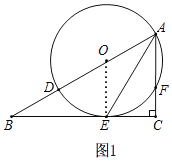
连接OE，∴OA=OE，

∴∠BAE=∠OEA，

∵∠BAE=30°，

∴∠OEA=30°，

∴∠AOE=∠BAE+∠OEA=60°，

在△BOE中，∠B=30°，

∴∠OEB=180°-∠B-∠BOE=90°，

∴OE⊥BC，

∵点E在⊙O上，

∴BC是⊙O的切线；

（2）如图2，

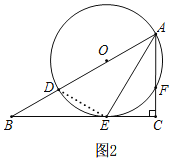
∵∠B=∠BAE=30°，

∴∠AEC=∠B+∠BAE=60°，

在Rt△ACE中，AC=3，sin∠AEC=，

∴AE=，

连接DE，∵AD是⊙O的直径，

∴∠AED=90°，

在Rt△ADE中，∠BAE=30°，cos∠DAE=，

∴AD=，

∴⊙O的半径r=AD=2；

（3）以A、O、E、F为顶点的四边形是菱形，理由：如图3，

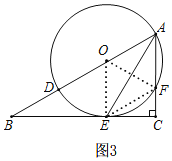
在Rt△ABC中，∠B=30°，

∴∠BAC=60°，

连接OF，∴OA=OF，

∴△AOF是等边三角形，

∴OA=AF，∠AOF=60°，

连接EF，OE，

∴OE=OF，

∵∠OEB=90°，∠B=30°，

∴∠AOE=90°+30°=120°，

∴∠EOF=∠AOE-∠AOF=60°，

∵OE=OF，

∴△OEF是等边三角形，

∴OE=EF，

∵OA=OE，

∴OA=AF=EF=OE，

∴四边形OAFE是菱形．