��Ŀ����
����Ŀ����֪��������A��B���㣬�ֱ��ʾ��40��20���ס�����ֻ���Ϸֱ��A��B����ͬʱ�����������߶�AB������3����λ����/����ٶ������˶��������B��ʱ�˶�ֹͣ�������߶�BA������5����λ����/����ٶ������˶���
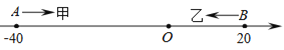
��1����ס��ҵ�һ������������ʾ������
��2����������ʱ���ס������28����λ���ȣ�
��3�����ҵ���A������̵�ͷ�ϼף��ٶȱ��ֲ��䣩�����ڼ���B��ǰ���ס����Ƿ����ٴ����������ܣ��������������ʾ�����������ܣ���˵�����ɣ�
���𰸡���1���ס��ҵ�һ���������ʾ������![]() ����2������4���11��ʱ���ס������28����λ���ȣ���3���ס��Ҳ����ٴ����������ɼ�����
����2������4���11��ʱ���ס������28����λ���ȣ���3���ס��Ҳ����ٴ����������ɼ�����
��������
��1�����������֪����һ������ʱ���������ߵ���·��Ϊ60���ݴ˽�һ���������ʱ�䲢�г������������ʱ�䣬Ȼ���һ�����㼴�ɣ�
��2���辭��y��ʱ�ס������28����λ���ȣ�Ȼ�������ǰ�����������������һ���������г�������⼴�ɣ�
��3����ס����ٴ���������ʻ![]() �룬Ȼ����������г����̣������ʱ��ʱ�䣬�ݴ��������ʻ·�̣������������жϼ���.
�룬Ȼ����������г����̣������ʱ��ʱ�䣬�ݴ��������ʻ·�̣������������жϼ���.
��1����ס��Ҿ���![]() ���һ��������
���һ��������
��![]() ��
��
��ã�![]() ��
��
��40+![]() =
=![]() ��
��
�𣺼ס��ҵ�һ���������ʾ������![]() ��
��
��2���辭��y��ʱ�ס������28����λ���ȣ�
��3y+5y=6028��3y+5y60=28��
��ã�y=4��y=11��
�𣺾���4���11��ʱ���ס������28����λ���ȣ�
��3������B��ǰ���ס��Ҳ����ٴ�������
�������£�
��ס����ٴ���������ʻ![]() �룬
�룬
��![]() ��
��
��ã�![]() ��
��
��![]() ,
,
��ס��Ҳ����ٴ�����.

 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�