题目内容
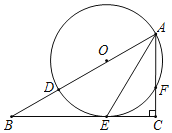
【题目】如图，已知A（﹣2，0），B（4，0），抛物线y=ax2+bx﹣1过A、B两点，并与过A点的直线y=﹣
x﹣1交于点C．
（1）求抛物线解析式及对称轴；
（2）在抛物线的对称轴上是否存在一点P，使四边形ACPO的周长最小？若存在，求出点P的坐标，若不存在，请说明理由；
（3）点M为y轴右侧抛物线上一点，过点M作直线AC的垂线，垂足为N．问：是否存在这样的点N，使以点M、N、C为顶点的三角形与△AOC相似，若存在，求出点N的坐标，若不存在，请说明理由．
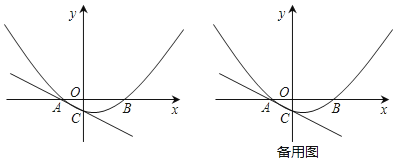
【答案】（1）抛物线解析式为：y=
，抛物线对称轴为直线x=1；（2）存在P点坐标为（1，﹣
）；（3）N点坐标为（4，﹣3）或（2，﹣1）
【解析】（1）由待定系数法求解即可；
（2）将四边形周长最小转化为PC+PO最小即可；
（3）利用相似三角形对应点进行分类讨论，构造图形．设出点N坐标，表示点M坐标代入抛物线解析式即可．
（1）把A（-2，0），B（4，0）代入抛物线y=ax2+bx-1，得
解得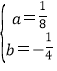
∴抛物线解析式为：y=
x2
x1
∴抛物线对称轴为直线x=-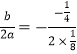
＝1
（2）存在
使四边形ACPO的周长最小，只需PC+PO最小
∴取点C（0，-1）关于直线x=1的对称点C′（2，-1），连C′O与直线x=1的交点即为P点．
设过点C′、O直线解析式为：y=kx
∴k=-
∴y=-x
则P点坐标为（1，-）
（3）当△AOC∽△MNC时，
如图，延长MN交y轴于点D，过点N作NE⊥y轴于点E
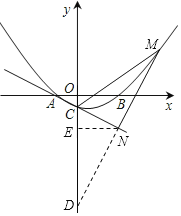
∵∠ACO=∠NCD，∠AOC=∠CND=90°
∴∠CDN=∠CAO
由相似，∠CAO=∠CMN
∴∠CDN=∠CMN
∵MN⊥AC
∴M、D关于AN对称，则N为DM中点
设点N坐标为（a，-a-1）
由△EDN∽△OAC
∴ED=2a
∴点D坐标为（0，-
a1）
∵N为DM中点
∴点M坐标为（2a，
a1）
把M代入y=x2x1，解得
a=4
则N点坐标为（4，-3）
当△AOC∽△CNM时，∠CAO=∠NCM
∴CM∥AB则点C关于直线x=1的对称点C′即为点N
由（2）N（2，-1）
∴N点坐标为（4，-3）或（2，-1）
