题目内容
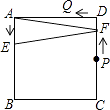
【题目】(1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4.点D是AB边上任意一点,则CD的最小值为 。
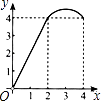
(2)如图②,在矩形ABCD中,AB=3,BC=4.点M、N分别在BD、BC上。求CM+MN的最小值.
(3)如图③,在矩形ABCD中,AB=3,BC=4.点E是AB边上的一点,且AE=2,点F是BC边上的任意一点。把△BEF沿EF翻折,点B对应点G,连接AG、CG.四边形AGCD的面积的最小值是 。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)根据点到直线的距离最小,再用三角形的面积即可得出结论;
(2)先根据轴对称确定出点M和N的位置,再利用面积求出CF,进而求出CE,最后用三角函数即可求出CM+MN的最小值;
(3)先确定出EG⊥AC时,四边形AGCD的面积最小,再用锐角三角函数求出点G到AC的距离,最后用面积之和即可得出结论.
(1)如图①,
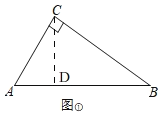
过点C作CD⊥AB于D,根据点到直线的距离垂线段最小,此时CD最小,
在Rt△ABC中,AC=3,BC=4,根据勾股定理得,AB=5,
∵![]() AC×BC=
AC×BC=![]() AB×CD,
AB×CD,
∴CD=![]() =
=![]() ,
,
故答案为:![]() ;
;
2)如图②,
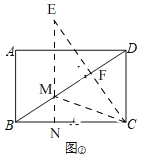
作出点C关于BD的对称点E,
过点E作EN⊥BC于N,交BD于M,连接CM,此时CM+MN=EN最小;
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=3,根据勾股定理得,BD=5,
∵CE⊥BC,
∴![]() BD×CF=
BD×CF=![]() BC×CD,
BC×CD,
∴CF=![]() =
=![]() ,
,
由对称得,CE=2CF=![]() ,
,
在Rt△BCF中,cos∠BCF=![]() =
=![]() ,
,
∴sin∠BCN=![]() ,
,
在Rt△CEN中,EN=CEsin∠BCE=![]() =
=![]() ;
;
即:CM+MN的最小值为![]() ;
;
(3)如图,
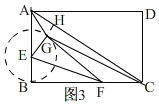
∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得,AC=5,
∵AB=3,AE=2,
∴点F在BC上的任何位置时,点G始终在AC的下方,
设点G到AC的距离为h,
∵S四边形AGCD=S△ACD+S△ACG=![]() AD×CD+
AD×CD+![]() AC×h=
AC×h=![]() ×4×3+
×4×3+![]() ×5×h=
×5×h=![]() h+6,
h+6,
∴要四边形AGCD的面积最小,即:h最小,
∵点G是以点E为圆心,BE=1为半径的圆上在矩形ABCD内部的一部分点,
∴EG⊥AC时,h最小,
由折叠知∠EGF=∠ABC=90°,
延长EG交AC于H,则EH⊥AC,
在Rt△ABC中,sin∠BAC=![]() ,
,
在Rt△AEH中,AE=2,sin∠BAC=![]() ,
,
∴EH=![]() ,AE=
,AE=![]() ,
,
∴h=EH-EG=![]() -1=
-1=![]() ,
,
∴S四边形AGCD最小=![]() h+6=
h+6=![]() ×
×![]() +6=
+6=![]() .
.

【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?