题目内容
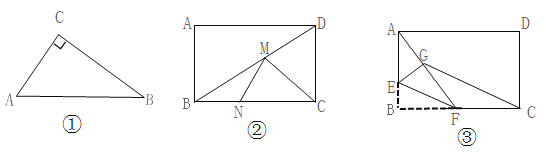
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.

【答案】(1)证明见解析;(2)24![]()
【解析】试题(1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;
(2)利用勾股定理得出AE的长,进而求出菱形的面积.
试题解析:(1)∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=![]() AD,EC=
AD,EC=![]() BC,
BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形,
又∵∠AEC=90°,
∴四边形AECF是矩形;
(2)在Rt△ABE中,AE=![]() ,
,
所以,S菱形ABCD=6×3![]() =18
=18![]() .
.

练习册系列答案
相关题目
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?