Question

如图，过反比例函数y=

4

x

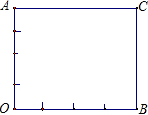
图象上一点A分别向x轴，y轴作垂线，垂足分别为点B，C，两条垂线与坐标轴所围成的图形为正方形，过点A的一次函数y=kx+1与x轴、y轴分别交于点D、E，作EF∥x轴，分别交AB和反比函数图象于点G、F，连接BF，AF．
（1）求点A的坐标和一次函数解析式；
（2）求四边形ADBF的面积；
（3）猜想线段DE和线段BF有怎样的关系，并加以证明．

Answer 1

（1）∵点A在反比例函数y=

4

x

图象上，
反比例函数比例系数为4，
则正方形ABOC的面积为4，
即OB×AB=4，
AB=OB=2，
A点坐标为（2，2）．
将A（2，2）代入y=kx+1得，2k+1=2，k=

1

2

，
函数解析式为y=

1

2

x+1．

（2）设E点坐标为（0，e），代入y=

1

2

x+1得，e=1．
由于EF∥x轴，
可得F点纵坐标为1，
将y=1代入y=

4

x

得，x=4，F点坐标为（4，1）．
设D点坐标为（d，0），代入y=

1

2

x+1得，0=

1

2

d+1，
d=-2，D点坐标为（-2，0）．
S_{四边形ADBF}=S_△ADB+S_△ABF=

1

2

×4×2+

1

2

×2×2=4+2=6．

（3）∵EF=DB=4，EF∥DB，
∴四边形DBFE为平行四边形，
则DE与BF平行且相等．