Question

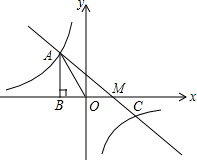
如图，P为x轴正半轴上一点，过点P作x轴的垂线，交函数y=

1

x

(x＞0)的图象于点A，交函数y=

4

x

(x＞0)的图象于点B，过点B作x轴的平行线，交y=

1

x

(x＞0)于点C，连接AC．
（1）当点P的坐标为（2，0）时，求△ABC的面积；
（2）当点P的坐标为（t，0）时，△ABC的面积是否随t值的变化而变化？

Answer 1

（1）根据题意，得点A、B的横坐标和点P的横坐标相等，即为2．
∵点A在函数y=

1

x

(x＞0)的双曲线上，
∴A点纵坐标是

1

2

，
∵点B在函数y=

4

x

(x＞0)的图象上
∴B点的纵坐标是2．
∴点C的纵坐标是2，
∵点C在函数y=

1

x

(x＞0)的双曲线上
∴C点横坐标是

1

2

．
∴AB=

3

2

，BC=

3

2

∴△ABC的面积是：

1

2

×

3

2

×

3

2

=

9

8

．

（2）根据（1）中的思路，可以分别求得点A（t，

1

t

），B（t，

4

t

），C（

t

4

，

4

t

）．
∴AB=

3

t

，BC=

3

4

t，
∴△ABC的面积是

9

8

．
∴△ABC的面积不会随着t的变化而变化．