Question

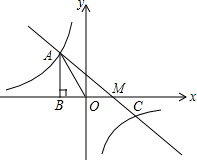
如图，已知双曲线y=

k

x

（k＞0）经过直角三角形OAB斜边OB和直角边AB上的点D、C，OA边在x轴上，若OD：DB=3：4，DE⊥OA，垂足为E，则
（1）OE：OA=______．
（2）△OAC的面积与△OCB的面积的比值是______．

Answer 1

（1）∵DE⊥x轴，BA⊥x轴，
∴∠DEO=∠BAO=90°，
∵∠DOE=∠BOA，
∴△DOE∽△BOA，
∴

OE

OA

=

OD

OD+DB

=

3

3+4

=

3

7

，即OE：OA=3：7；

（2）设△OAC面积为x，根据反比例函数k的意义得到三角形ODE面积为x，
∵△DOE∽△BOA，
∴三角形DOE与三角形BOA面积之比为9：49，
∴三角形BOA面积为

49

9

x，即三角形BOC面积为

49

9

x-x=

40

9

x，
则△OAC的面积与△OCB的面积的比值是9：40．
故答案为：（1）3：7；（2）9：40．