题目内容
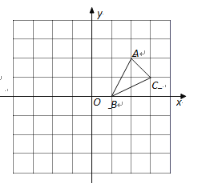
【题目】在一场篮球比赛中,一名球员在关键时刻投出一球,已知球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,已知篮球运行的轨迹为抛物线,篮圈中心距离地面3.19米.
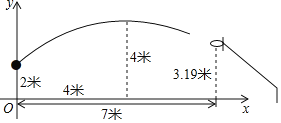
(1)以地面为x轴,篮球出手时垂直地面所在直线为y轴建立平面直角坐标系,求篮球运行的抛物线轨迹的解析式;
(2)通过计算,判断这个球员能否投中?
【答案】(1)![]() ;(2)不能投中
;(2)不能投中
【解析】
(1)根据题意可得抛物线的顶点,设函数的顶点式,再将(0,2)代入,求得二次项系数,从而可得抛物线的解析式;
(2)判断当x=7时,函数值是否等于3.19即可.
(1)依题意得抛物线顶点为(4,4),
则设抛物线的解析式为y=a(x﹣4)2+4
依题意得抛物线经过点(0,2)
∴a(0﹣4)2+4=2
解得![]()
∴抛物线的解析式为![]()
(2)当x=7时,![]() =
=![]()
∴这个球员不能投中.

练习册系列答案
相关题目