Question

【题目】 如图，E为正方形ABCD边AB上一动点（不与A重合），AB=4，将△DAE绕着点A逆时针旋转90°得到△BAF，再将△DAE沿直线DE折叠得到△DME．下列结论：①连结AM，则AM∥FB；②连结FE，当F、E、M共线时，AE=4-4；③连结EF、EC、FC，若△FEC是等腰三角形，则AE=4-4；④连结EF，设FC、ED交于点O，若FE平分∠BFC，则O是FC的中点，且AE=2-2，其中正确的个数有（　　）个．

A.4B.3C.2D.1

Answer 1

【答案】A

【解析】

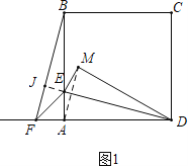
①正确．如图1中，连接AM，延长DE交BF于J．想办法证明BF⊥DJ，AM⊥DJ即可．

②正确．如图2中，当F、E、M共线时，易证∠DEA=∠DEM=67.5°，在MD上取一点J，使得ME=MJ，连接EJ，设AE=EM=MJ=x，则EJ=JD=x，构建方程即可解决问题．

③正确．如图3中，连接EC，CF，当EF=CE时，设AE=AF=m，利用勾股定理构建方程即可解决问题．

④正确．如图4中，当OF=OC时，设AE=AF=n．根据tan∠CFD=tan∠EDA，构建方程即可解决问题．

解：①如图1中，连接AM，延长DE交BF于J．

∵四边形ABCD是正方形，

∴AB=AD．∠DAE=∠BAF=90°，

∵AE=AF，

∴△BAF≌△DAE（SAS），

∴∠ABF=∠ADE，

∵∠ADE+∠AED=90°，∠AED=∠BEJ，

∴∠BEJ+∠EBJ=90°，

∴∠BJE=90°，

∴DJ⊥BF，

由翻折可知：EA=EM，DM=DA，

∴DE垂直平分线段AM，

∴BF∥AM，故①正确，

②如图2中，当F、E、M共线时，易证∠DEA=∠DEM=67.5°，

在MD上取一点J，使得ME=MJ，连接EJ，

∵∠MEJ=∠MJE=45°，

∴∠JED=∠JDE=22.5°，

∴EJ=JD，设AE=EM=MJ=x，则EJ=JD=x，

则有x+x=4，

∴x=4-4，

∴AE=4-4故②正确，

③如图3中，连接EC，CF，当EF=CE时，设AE=AF=m，

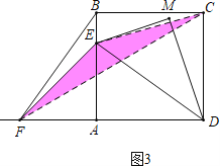
则有：2m2=42+（4-m）2，

∴m=4-4或-4-4（舍弃），

∴AE=4-4，故③正确，

④如图4中，当OF=OC时，设AE=AF=n．

∵∠FDC=90°，OF=OC，

∴OF=OD，

∴∠OFD=∠ODF，

∴tan∠CFD=tan∠EDA，

，=，

∴n=2-2或-2-2（舍弃），

∴AE=2-2，故④正确．

故选：A．