题目内容
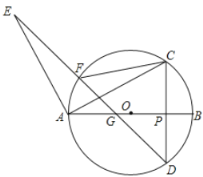
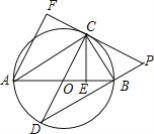
【题目】 如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)若![]() ,⊙O的面积为12π,求PF的长.
,⊙O的面积为12π,求PF的长.
【答案】(1)详见解析;(2)详见解析;(3)7
【解析】
(1)根据切线的性质得到OC⊥CP,证明OC∥AF,根据平行线的性质、等腰三角形的性质证明;
(2)根据圆周角定理得到∠ACB=90°,证明△CEB∽△CBP,根据相似三角形的性质证明结论;
(3)设CE=3x,根据题意用x表示出CP、CB,根据相似三角形的性质列出方程,解方程求出x,根据角平分线的性质得到CF=CE,结合图形计算,得到答案.
(1)证明:∵CP是⊙O的切线,
∴OC⊥CP,
∵AF⊥PC,
∴OC∥AF,
∴∠FAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠FAC=∠OAC,即AC平分∠FAB;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,即∠CAB+∠ABC=90°,
∵EC⊥OB,
∴∠ECB+∠ABC=90°,
∴∠CAB=∠ECB,
∵CP是⊙O的切线,
∴∠CAB=∠BCP,
∴∠ECB=∠BCP,
∵CD是⊙O的直径,
∴∠CBD=90°,
∴∠CEB=∠CBP,又∠ECB=∠BCP,
∴△CEB∽△CBP,
∴![]() =
=![]() ,即BC2=CECP;
,即BC2=CECP;
(3)解:设CE=3x,
∵![]() ,
,
∴CP=4x,
∵BC2=CECP,
∴BC=2![]() x,
x,
由勾股定理得,BE=![]() =
=![]() x,
x,
∵⊙O的面积为12π,
∴⊙O的半径为2![]() ,即AB=4
,即AB=4![]() ,
,
∵∠ACB=90°,CE⊥AB,
∴BC2=BEAB,即(2![]() x)2=
x)2=![]() x4
x4![]() ,
,
解得,x=1,
则CE=3,CP=4,
∵AC平分∠FAB,AF⊥PC,EC⊥OB,
∴CF=CE=3,
∴PF=CF+CP=7.

【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
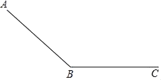
A.270B.280C.375D.450