题目内容
【题目】如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．
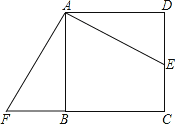
（1）旋转中心是点 ，旋转角度是 度；
（2）若连结EF，则△AEF是 三角形；并证明
【答案】（1）A；90；（2）△AEF是等腰直角三角形，
【解析】
试题（1）利用旋转的定义直接填写即可；
（2）可证明△ADE≌△ABF，可得出AE=AF，且可求得∠EAF=90°；
试题解析：（1）由旋转的定义可知旋转中心为A，AD从AD到AB，可知旋转了90°．
（2）△AEF是等腰直角三角形，
理由如下：
∵四边形ABCD是正方形，
∴∠DAB=90°，
∵△ADE经顺时针旋转后与△ABF重合，
∴△ADE≌△ABF，∠DAB=∠EAF=90°，
∴AE=AF，
∴△AEF是等腰直角三角形；
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
【题目】某企业生产了一款健身器材，可通过实体店和网上商店两种途径进行销售，销售了一段时间后，该企业对这种健身器材的销售情况进行了为期30天的跟踪调查，其中实体店的日销售量y1(套)与时间x(x为整数，单位:天)的部分对应值如下表所示:
时间x(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量y(套) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数，单位:天)的函数关系为
，则在跟踪调查的30天中，设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式；当x为何值时，日销售总量y达到最大，并写出此时的最大值.
【题目】已知二次函数y＝ax2＋bx＋c（a≠0），该函数y与自变量x的部分对应值如下表：
x | … | 1 | 2 | 3 | … |
y | … | 0 | ﹣1 | 0 | … |
(1)求该二次函数的表达式；
(2)不等式ax2＋bx＋c＞0的解集为 ；
不等式ax2＋bx＋c＜3的解集为 .