题目内容
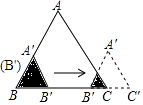
【题目】如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=40°，N是弧MB的中点，P是直径AB上的一动点，PM+PN的最小值为（ ）
A.4 
+1
B.4
C.4 
+1
D.5
【答案】B
【解析】解：作点N关于AB的对称点C，连接MC交AB于点P，则P点就是所求作的点．
此时PM+PN最小，且等于MC的长．
连接OM，OC，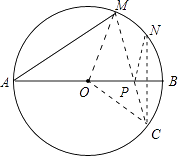
∵∠MAB=40°，
∴∠MOB=80°，
∴ 
的度数是80°，
则 
的度数是40°，
根据垂径定理得 
的度数是40°，
则∠NOC=120°，
∵AB=8
∴OM=OC=4，
∴∠OAM=∠OMC=30°，
∴MC=4 
．
∴PM+PN的最小值为4 ，
故选B．
作点N关于AB的对称点C，连接MC交AB于点P，则P点就是所求作的点，求出∠COM=120°，进而求出CM的长，CM的长度即PM+PN的最小值．
练习册系列答案
相关题目
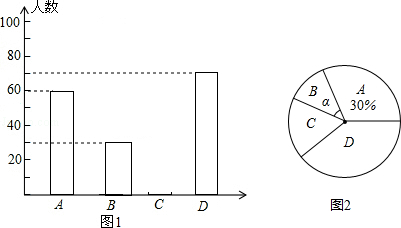
【题目】今年4月23日，是第16个世界读书日．某校为了解学生每周课余自主阅读的时间，在本校随机抽取若干名学生进行问卷调查，现将调查结果绘制成如图不完整的统计图表，请根据图表中的信息解答下列问题
组别 | 学习时间x（h） | 频数（人数） |
A | 0＜x≤1 | 8 |
B | 1＜x≤2 | 24 |
C | 2＜x≤3 | 32 |
D | 3＜x≤4 | n |
E | 4小时以上 | 4 |
（1）表中的n= ， 中位数落在组，扇形统计图中B组对应的圆心角为°；
（2）请补全频数分布直方图；
（3）该校准备召开利用课余时间进行自主阅读的交流会，计划在E组学生中随机选出两人进行经验介绍，已知E组的四名学生中，七、八年级各有1人，九年级有2人，请用画树状图法或列表法求抽取的两名学生都来自九年级的概率．
